Figures 1-3
 Figure 1
Pure modes. In the absence of sources, the growing mode of the
rest frame temperature perturbation matches onto a cosine acoustic
oscillation inside the horizon, whereas the decaying mode matches onto
a sine oscillation. The oscillator response to an external source is
constructed by Greens method from these homogeneous solutions and
transformed into the Newtonian frame with Eq.~(9).
Figure 1
Pure modes. In the absence of sources, the growing mode of the
rest frame temperature perturbation matches onto a cosine acoustic
oscillation inside the horizon, whereas the decaying mode matches onto
a sine oscillation. The oscillator response to an external source is
constructed by Greens method from these homogeneous solutions and
transformed into the Newtonian frame with Eq.~(9).
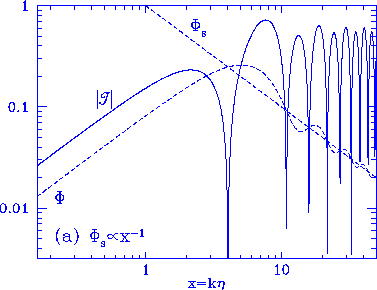

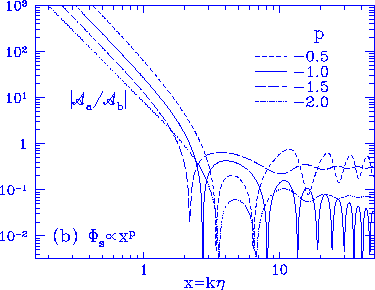 Figure 2
Compensation and isocurvature fluctuations.
(a) Baryon isocurvature model ($\Phi_s \propto x^{-1}$). Outside
the horizon $x \simlt 1$, backreaction from the photons cancels the
contribution of the source to the curvature fluctuation. Inside
the horizon, pressure prevents significant metric contributions
from the photon-baryon fluid and $\Phi \rightarrow \Phi_s$. (b)
For source functions $\Phi_s \propto x^{p}$, the ratio of $\RF_a$
to $\RF_b$ amplitudes decreases due to feedback. This leaves the
acoustic oscillation mainly in the sine mode at $x \gg 1$.
Figure 2
Compensation and isocurvature fluctuations.
(a) Baryon isocurvature model ($\Phi_s \propto x^{-1}$). Outside
the horizon $x \simlt 1$, backreaction from the photons cancels the
contribution of the source to the curvature fluctuation. Inside
the horizon, pressure prevents significant metric contributions
from the photon-baryon fluid and $\Phi \rightarrow \Phi_s$. (b)
For source functions $\Phi_s \propto x^{p}$, the ratio of $\RF_a$
to $\RF_b$ amplitudes decreases due to feedback. This leaves the
acoustic oscillation mainly in the sine mode at $x \gg 1$.
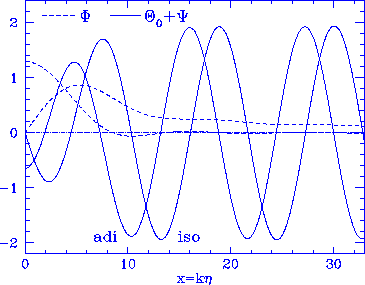 Figure 3
{Driven oscillations. The self-gravity of the photon-baryon fluid
drives a cosine oscillation for adiabatic initial conditions (thin lines)
and a sine oscillation (thick lines) for isocurvature initial
conditions. The adiabatic model has $\Phi_s(x_i)=0$ and
$\Phi_{\gamma b}(x_i)\ne0$. The isocurvature model is the baryonic
model of Eq.~(19). The dashed lines show the full potential, the solid
lines the effective temperature. In both cases the amplitude
in $\Theta_0+\Psi$ increase during the first few oscillations, as described
in \S2.5.
Figure 3
{Driven oscillations. The self-gravity of the photon-baryon fluid
drives a cosine oscillation for adiabatic initial conditions (thin lines)
and a sine oscillation (thick lines) for isocurvature initial
conditions. The adiabatic model has $\Phi_s(x_i)=0$ and
$\Phi_{\gamma b}(x_i)\ne0$. The isocurvature model is the baryonic
model of Eq.~(19). The dashed lines show the full potential, the solid
lines the effective temperature. In both cases the amplitude
in $\Theta_0+\Psi$ increase during the first few oscillations, as described
in \S2.5.
 Figure 1
Figure 1
 Figure 1
Figure 1


 Figure 2
Figure 2
 Figure 3
Figure 3