Figures 4-6
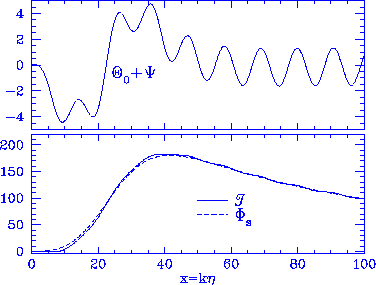 Figure 4
Forced oscillations. Inside the horizon, the regulatory effects of
photon-baryon self-gravity become ineffective. A source that peaks
at $x=k\eta\gg 1$ can produce complicated forced oscillations in the
fluid. The intrinsic temperature fluctuation $\RF\approx\Theta_0$
suffers a large unobservable offset $-\Psi_s$ (bottom panel) which is
removed by the redshift in the effective temperature $\Theta_0+\Psi$
(top panel). Notice that the fundamental period $kr_s = 2\pi$ or
$x\simeq 10.9$ is still clearly apparent for this slowly-varying source.
Figure 4
Forced oscillations. Inside the horizon, the regulatory effects of
photon-baryon self-gravity become ineffective. A source that peaks
at $x=k\eta\gg 1$ can produce complicated forced oscillations in the
fluid. The intrinsic temperature fluctuation $\RF\approx\Theta_0$
suffers a large unobservable offset $-\Psi_s$ (bottom panel) which is
removed by the redshift in the effective temperature $\Theta_0+\Psi$
(top panel). Notice that the fundamental period $kr_s = 2\pi$ or
$x\simeq 10.9$ is still clearly apparent for this slowly-varying source.
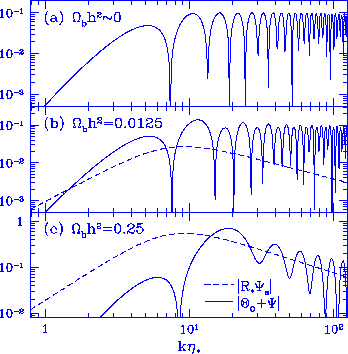 Figure 5
Baryon drag and relative peak heights.
Baryons displace the zero point of the oscillation by $- R\Psi$.
For a near BBN baryon content (center panel),
the displacement is smaller than the oscillation itself leading to
alternating peak heights in the rms. For a much larger baryon content,
the photons oscillate around a strongly displaced zero point.
Figure 5
Baryon drag and relative peak heights.
Baryons displace the zero point of the oscillation by $- R\Psi$.
For a near BBN baryon content (center panel),
the displacement is smaller than the oscillation itself leading to
alternating peak heights in the rms. For a much larger baryon content,
the photons oscillate around a strongly displaced zero point.
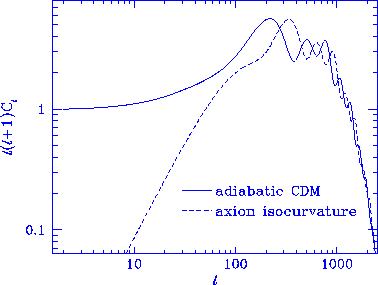 Figure 6
Diffusion damping. Although adiabatic
and isocurvature models predict acoustic oscillations in different
positions, they both suffer diffusion damping in the same way.
The damping length is fixed by background assumptions, here
$\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$ and standard recombination.
These calculations were performed
using a full numerical integration of the Boltzmann equation with
the code of Sugiyama (1995) as were results in Figs.~7,8,10,11.
Figure 6
Diffusion damping. Although adiabatic
and isocurvature models predict acoustic oscillations in different
positions, they both suffer diffusion damping in the same way.
The damping length is fixed by background assumptions, here
$\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$ and standard recombination.
These calculations were performed
using a full numerical integration of the Boltzmann equation with
the code of Sugiyama (1995) as were results in Figs.~7,8,10,11.
 Figure 4
Figure 4
 Figure 4
Figure 4
 Figure 5
Figure 5
 Figure 6
Figure 6