Figures 7-9
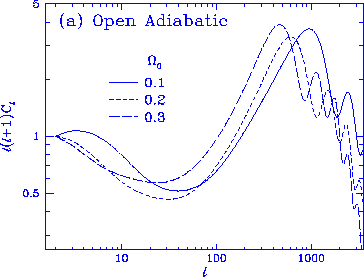
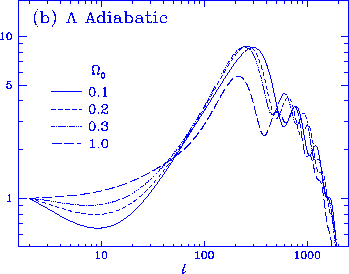
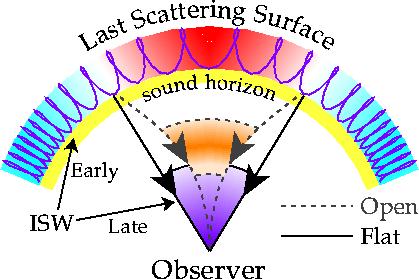 Figure 7
Location of the peaks. The location of the peaks is
determined by the angle the sound horizon subtends at last scattering.
In an open universe, geodesic deviation makes this angle much smaller
than in a flat universe. As this
angle involves a ratio of the sound horizon to the (angular
diameter) distance to
last scattering, distance scale changes through $\Lambda$ and $h$
have little effect on its angle.
The drop in the lowest multipoles for the open
$\Omega_0=0.1$ is due to the lack
of supercurvature scale power in the otherwise
scale invariant initial conditions assumed here. Models here
have $h=0.5$ and $\Omega_b=0.05$.
Figure 7
Location of the peaks. The location of the peaks is
determined by the angle the sound horizon subtends at last scattering.
In an open universe, geodesic deviation makes this angle much smaller
than in a flat universe. As this
angle involves a ratio of the sound horizon to the (angular
diameter) distance to
last scattering, distance scale changes through $\Lambda$ and $h$
have little effect on its angle.
The drop in the lowest multipoles for the open
$\Omega_0=0.1$ is due to the lack
of supercurvature scale power in the otherwise
scale invariant initial conditions assumed here. Models here
have $h=0.5$ and $\Omega_b=0.05$.
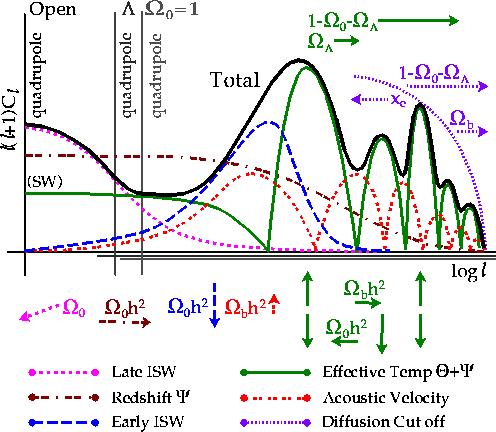 Figure 8
Parameter sensitivity. A schematic representation based
on a scale invariant adiabatic scalar model. Features in
an open model are shifted to significantly smaller angles compared with
$\Lambda$ and $\Omega_0=1$ models, represented here as a shift
in the $\ell$ axis. Isocurvature models behave similarly with
respect to the acoustic oscillations save that the peaks are
90 degrees out of phase. The spectrum may also be tilted by changing
the initial power spectrum from the scale invariant assumption.
Figure 8
Parameter sensitivity. A schematic representation based
on a scale invariant adiabatic scalar model. Features in
an open model are shifted to significantly smaller angles compared with
$\Lambda$ and $\Omega_0=1$ models, represented here as a shift
in the $\ell$ axis. Isocurvature models behave similarly with
respect to the acoustic oscillations save that the peaks are
90 degrees out of phase. The spectrum may also be tilted by changing
the initial power spectrum from the scale invariant assumption.
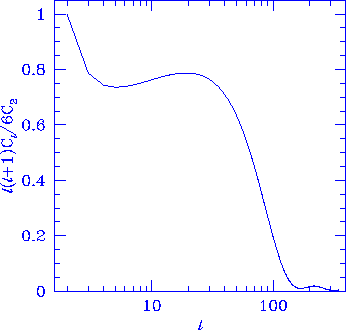 Figure 9
Gravitational Wave ISW Effect. The metric distortion
caused by a gravitational wave induces a redshift/dilation effect
on CMB photons. The spectrum is cut off below the angle subtended
by the horizon at last scattering since gravity waves only affect
free streaming photons significantly. Due to the signature of the
metric distortion, it originates as a source of the quadrupole anisotropy.
Figure 9
Gravitational Wave ISW Effect. The metric distortion
caused by a gravitational wave induces a redshift/dilation effect
on CMB photons. The spectrum is cut off below the angle subtended
by the horizon at last scattering since gravity waves only affect
free streaming photons significantly. Due to the signature of the
metric distortion, it originates as a source of the quadrupole anisotropy.


 Figure 7
Figure 7


 Figure 7
Figure 7
 Figure 8
Figure 8
 Figure 9
Figure 9