Gauge

General relativity leaves us the freedom to choose the coordinate system in which to represent perturbations from complete homogeneity and isotropy. This leads to gauge freedom or gauge ambiguity that is often a source of confusion for the uninitiated.

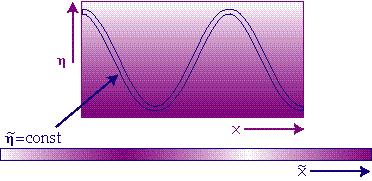
Practically speaking, a gauge choice involves fixing the constant-time hypersurfaces and the spatial grid of these surfaces. Depending on how we make these choices the representation of density (from time slicing) and velocity (from gridding) perturbations change. Let us see how this works. Suppose the universe were in fact perfectly homogeneous and isotropic:

Figure: Gauge Ambiguity from Hu (1995)

The density decreases with time due to the expansion. Now let us choose a surface that is temporally warped from the cosmic frame (tilde frame). On this surface, the background evolution of the density looks like a plane wave density perturbation! Thus the numerical values of what we call a density perturbation change even though the physical situation does not.

So long as the coordinate system is fully specified, there is no problem in choosing whatever system we like. The best choice depends on what the aim of the calculation is. The rest frame of the matter and variants, employed in the synchronous and comoving or total matter gauges, are the simplest to calculate in. These may be thought of as "Lagrangian" coordinates. When calculational problems are not an issue, a more "Eulerian" choice such as the Newtonian (shear free) gauge often clarifies the underlying physical processes. This particular gauge also has the benefits in that its non-relativistic limit reduces to ordinary Newtonian gravity and hence our intuition for things like potential wells can be carried over directly. This is the choice made for this review.