Figures 4-6
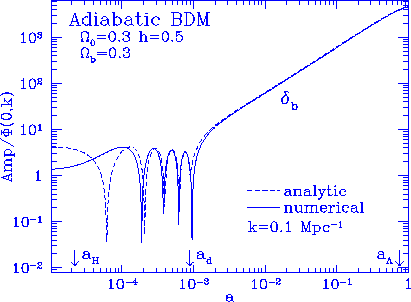 Figure 4
Baryon fluctuation time evolution. The baryon
density fluctuation $\delta_b$ follows the photons before
the drag epoch $a_d$ yielding a simple oscillatory form
for $a_H \ll a \ll a_d$. The Silk damping length is
given by the diffusion length at the drag epoch. The portion of
the baryon fluctuations that enter the growing mode is dominated
by the velocity perturbation at the drag epoch
$a_d$ due to the velocity overshoot effect (see also \Figno\velov).
Since a flat $\Lambda$ model is chosen here, the growth rate is
slowed by the rapid expansion for $a \simgt a_\Lambda =
(\Omega_0/\Omega_\Lambda)^{1/3}$.
Figure 4
Baryon fluctuation time evolution. The baryon
density fluctuation $\delta_b$ follows the photons before
the drag epoch $a_d$ yielding a simple oscillatory form
for $a_H \ll a \ll a_d$. The Silk damping length is
given by the diffusion length at the drag epoch. The portion of
the baryon fluctuations that enter the growing mode is dominated
by the velocity perturbation at the drag epoch
$a_d$ due to the velocity overshoot effect (see also \Figno\velov).
Since a flat $\Lambda$ model is chosen here, the growth rate is
slowed by the rapid expansion for $a \simgt a_\Lambda =
(\Omega_0/\Omega_\Lambda)^{1/3}$.
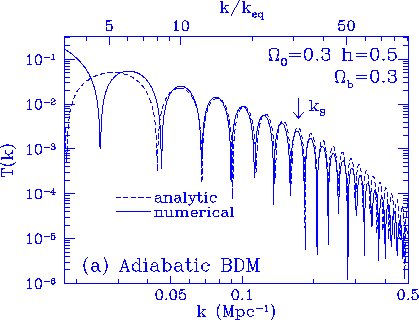
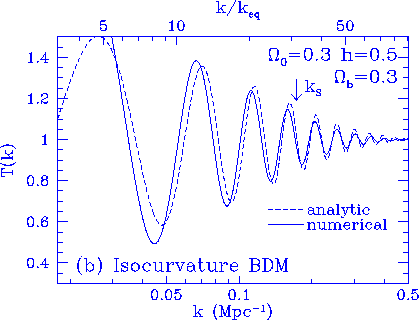
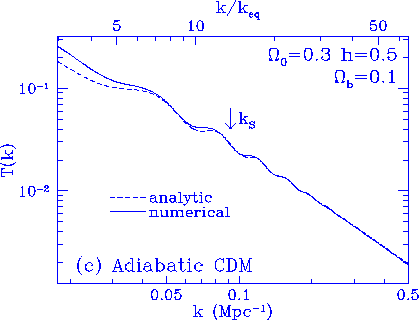 Figure 5
Matter transfer function. The analytic estimates of the intrinsic
acoustic amplitude is a good approximation for $k \gg k_{eq}$.
The Silk damping scale is adequately approximated although
its value is underestimated by $\sim 10\%$. For isocurvature
BDM and adiabatic CDM, the acoustic contributions do not dominate
the small scale fluctuations. We have added in the contributions
from the initial entropy fluctuations and the cold dark matter
potentials according to the analytic treatment of Appendix E.
Figure 5
Matter transfer function. The analytic estimates of the intrinsic
acoustic amplitude is a good approximation for $k \gg k_{eq}$.
The Silk damping scale is adequately approximated although
its value is underestimated by $\sim 10\%$. For isocurvature
BDM and adiabatic CDM, the acoustic contributions do not dominate
the small scale fluctuations. We have added in the contributions
from the initial entropy fluctuations and the cold dark matter
potentials according to the analytic treatment of Appendix E.
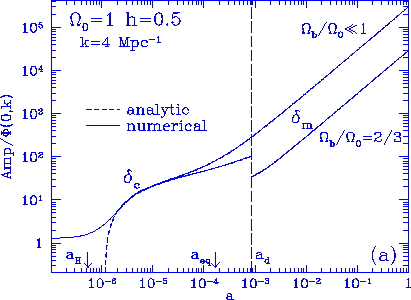
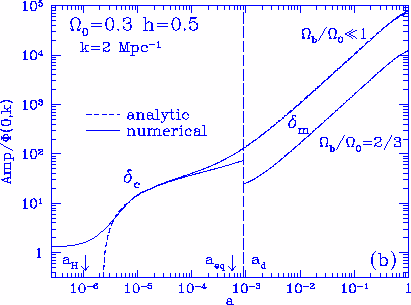 Figure 6
CDM and matter fluctuation
time evolution. The cold dark
matter fluctuations are constant outside the horizon scale and experience
a boost into a logarithmically growing mode at horizon
crossing in the radiation dominated
epoch.
Between equality
and the drag epoch, the presence of baryons suppress the growth rate
of CDM fluctuations [see eqn.~(7)].
By lowering $\Omega_0 h^2$, this region of suppression can
be reduced for fixed $\Omega_b/\Omega_0$, {\it cf.} (a) and (b).
After the drag epoch, we plot $\delta_m = (\delta_b\rho_b +
\delta_c\rho_c)/(\rho_b+\rho_c)$ rather than $\delta_c$ since
the two components thereafter contribute similarly to the
total growth.
Baryons also lower the contribution of $\delta_c$ to $\delta_m$ at the
drag epoch.
Figure 6
CDM and matter fluctuation
time evolution. The cold dark
matter fluctuations are constant outside the horizon scale and experience
a boost into a logarithmically growing mode at horizon
crossing in the radiation dominated
epoch.
Between equality
and the drag epoch, the presence of baryons suppress the growth rate
of CDM fluctuations [see eqn.~(7)].
By lowering $\Omega_0 h^2$, this region of suppression can
be reduced for fixed $\Omega_b/\Omega_0$, {\it cf.} (a) and (b).
After the drag epoch, we plot $\delta_m = (\delta_b\rho_b +
\delta_c\rho_c)/(\rho_b+\rho_c)$ rather than $\delta_c$ since
the two components thereafter contribute similarly to the
total growth.
Baryons also lower the contribution of $\delta_c$ to $\delta_m$ at the
drag epoch.
 Figure 4
Figure 4
 Figure 4
Figure 4


 Figure 5
Figure 5

 Figure 6
Figure 6