Figures 10-12
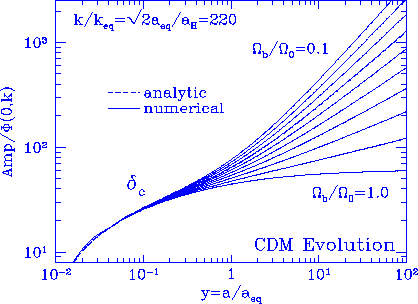 Figure 10
CDM evolution in the Compton drag epoch.
If baryons contribute a significant fraction
of the total matter density, CDM growth will be slowed between equality
and the drag epoch. Held by Compton drag, the baryons do not contribute
their self-gravity. For the numerical results, we choose a model that
never recombined so that $a_d \gg a_{eq}$.
Figure 10
CDM evolution in the Compton drag epoch.
If baryons contribute a significant fraction
of the total matter density, CDM growth will be slowed between equality
and the drag epoch. Held by Compton drag, the baryons do not contribute
their self-gravity. For the numerical results, we choose a model that
never recombined so that $a_d \gg a_{eq}$.
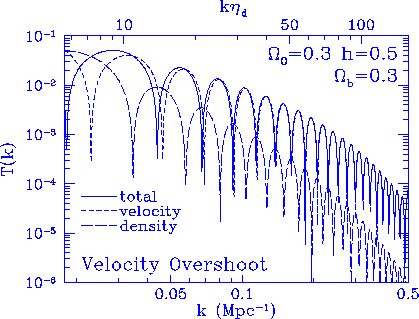 Figure 11
Velocity overshoot effect. Below the horizon at the drag epoch
$k\eta_d \gg 1$, the acoustic velocity at $z_d$ dominates the growing
mode and hence the final transfer function. Near the horizon, the
acoustic density becomes comparable and shifts the zero points of
the oscillation.
Figure 11
Velocity overshoot effect. Below the horizon at the drag epoch
$k\eta_d \gg 1$, the acoustic velocity at $z_d$ dominates the growing
mode and hence the final transfer function. Near the horizon, the
acoustic density becomes comparable and shifts the zero points of
the oscillation.
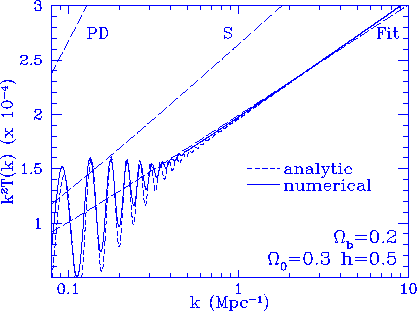 Figure 12
Adiabatic CDM transfer function in a high $\Omega_b/\Omega_0=2/3$ case.
The analytic solution is essentially exact
in the small scale limit. Simple fits based on the BBKS form
can cause large errors at the small scale: PD (Peacock \& Dodds 1994)
and S (Sugiyama 1995).
The fitting function developed here [see equation
\Edis\EeqnScaling] works at the $1\%$ level even for this extreme case.
Figure 12
Adiabatic CDM transfer function in a high $\Omega_b/\Omega_0=2/3$ case.
The analytic solution is essentially exact
in the small scale limit. Simple fits based on the BBKS form
can cause large errors at the small scale: PD (Peacock \& Dodds 1994)
and S (Sugiyama 1995).
The fitting function developed here [see equation
\Edis\EeqnScaling] works at the $1\%$ level even for this extreme case.
 Figure 10
Figure 10
 Figure 10
Figure 10
 Figure 11
Figure 11
 Figure 12
Figure 12