Figures
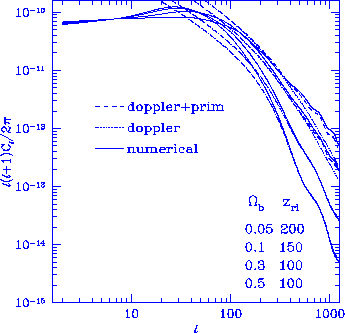 Figure 1
Doppler effect in reionized CDM models ($\Omega_0=1$, $h=0.5$, $n=1$).
For late ionization models $z_{\rm ri} \simlt z_d$,
the analytic estimate
which involves the neglect of Compton drag is an excellent approximation
to the numerical results at small scales. For low $\Omega_b h^2$ models,
the optical depth between $z_{\rm ri}$ at which the universe becomes fully
ionized and the present is insufficient to erase completely the primary
signal from standard recombination. The total effect is thus described
by adding $e^{-2\tau}$ of the standard recombination result to the
Doppler effect. Here and in Figs.~3,4,5 the relative normalization
is fixed by the amplitude of the matter power spectrum.
Figure 1
Doppler effect in reionized CDM models ($\Omega_0=1$, $h=0.5$, $n=1$).
For late ionization models $z_{\rm ri} \simlt z_d$,
the analytic estimate
which involves the neglect of Compton drag is an excellent approximation
to the numerical results at small scales. For low $\Omega_b h^2$ models,
the optical depth between $z_{\rm ri}$ at which the universe becomes fully
ionized and the present is insufficient to erase completely the primary
signal from standard recombination. The total effect is thus described
by adding $e^{-2\tau}$ of the standard recombination result to the
Doppler effect. Here and in Figs.~3,4,5 the relative normalization
is fixed by the amplitude of the matter power spectrum.
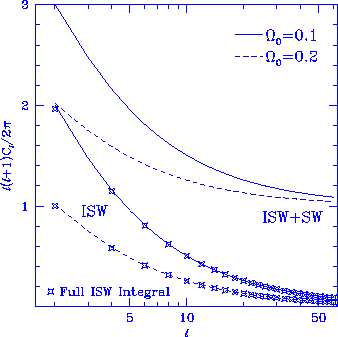 Figure 2
Weak coupling approximation for the $\Lambda$ ISW effect.
The analytic approximation based on crest-trough cancellation
traces the full ISW integral to high accuracy and accounts
for the falling ISW spectrum.
As $\Omega_0$ increases, the relative contribution of the ISW effect
decreases in comparison to the Sachs-Wolfe (SW) effect, arbitrarily
normalized to unity.
Here we have chosen a pure power law
$P(k) \propto k$ power spectrum.
Figure 2
Weak coupling approximation for the $\Lambda$ ISW effect.
The analytic approximation based on crest-trough cancellation
traces the full ISW integral to high accuracy and accounts
for the falling ISW spectrum.
As $\Omega_0$ increases, the relative contribution of the ISW effect
decreases in comparison to the Sachs-Wolfe (SW) effect, arbitrarily
normalized to unity.
Here we have chosen a pure power law
$P(k) \propto k$ power spectrum.
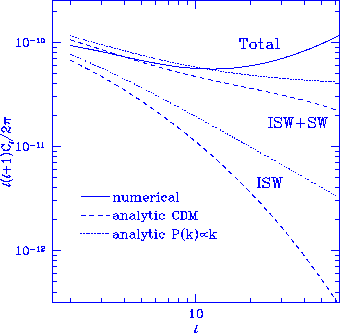 Figure 3
Comparison
with numerical integration (thick solid lines)
shows that at large scales, where
$\Lambda$ ISW and Sachs-Wolfe (SW) contributions dominate the anisotropy,
analytic formulae (thick dashed lines)
adequately describe the total anisotropy. At small
scales, the curves depart from the prediction due to the
early ISW effect and acoustic contributions (Hu \& Sugiyama 1995a).
Here we have chosen a high $h=1.0$, low $\Omega_0=0.1$
model to minimize these effects. Also
plotted in thin dotted lines is the analytic prediction for a pure
$P(k) \propto k$ power spectrum with the same normalization at large
scales.
Figure 3
Comparison
with numerical integration (thick solid lines)
shows that at large scales, where
$\Lambda$ ISW and Sachs-Wolfe (SW) contributions dominate the anisotropy,
analytic formulae (thick dashed lines)
adequately describe the total anisotropy. At small
scales, the curves depart from the prediction due to the
early ISW effect and acoustic contributions (Hu \& Sugiyama 1995a).
Here we have chosen a high $h=1.0$, low $\Omega_0=0.1$
model to minimize these effects. Also
plotted in thin dotted lines is the analytic prediction for a pure
$P(k) \propto k$ power spectrum with the same normalization at large
scales.
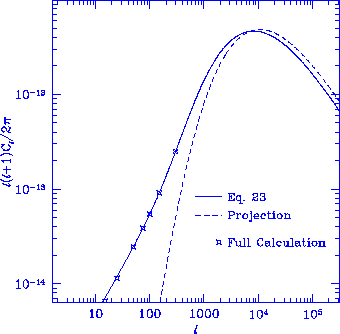 Figure 4
Comparison of different approximations for evaluating the
Vishniac effect for
a standard CDM model ($\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$) normalized
to COBE $(Q_{\rm rms-PS} = 20\mu {\rm K})$.
The cancellation approximation of Eq.~(23) matches
the full integral of Eq.~(22) extremely well, whereas
the projection of the r.m.s.~spatial fluctuation
(Efstathiou 1988) does not.
Figure 4
Comparison of different approximations for evaluating the
Vishniac effect for
a standard CDM model ($\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$) normalized
to COBE $(Q_{\rm rms-PS} = 20\mu {\rm K})$.
The cancellation approximation of Eq.~(23) matches
the full integral of Eq.~(22) extremely well, whereas
the projection of the r.m.s.~spatial fluctuation
(Efstathiou 1988) does not.
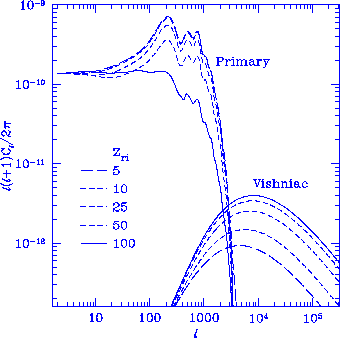 Figure 5
Primary and Vishniac contributions for
a range of possible ionization histories in the standard CDM model
(see Fig.~4). Note that even for
minimally ionized $z_{\rm ri}=5-10$, where first order
anisotropies are nearly indistinguishable from the standard
recombination case,
the Vishniac effect contributes a significant fraction of its total
in temperature fluctuations.
Because standard CDM has more small scale power than measurements suggest,
we
expect these calculations to be an upper limit for CDM-like models.
Figure 5
Primary and Vishniac contributions for
a range of possible ionization histories in the standard CDM model
(see Fig.~4). Note that even for
minimally ionized $z_{\rm ri}=5-10$, where first order
anisotropies are nearly indistinguishable from the standard
recombination case,
the Vishniac effect contributes a significant fraction of its total
in temperature fluctuations.
Because standard CDM has more small scale power than measurements suggest,
we
expect these calculations to be an upper limit for CDM-like models.
 Figure 1
Figure 1
 Figure 1
Figure 1
 Figure 2
Figure 2
 Figure 3
Figure 3
 Figure 4
Figure 4
 Figure 5
Figure 5