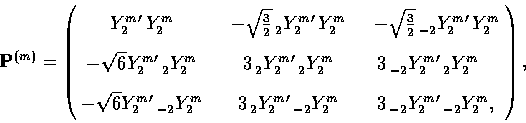Next: Normal Modes
Up: Boltzmann Equation
Previous: Boltzmann Equation
The gravitational term 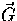 is easily evaluated from the Euler-Lagrange equations
for the motion of a massless particle in the background given by
is easily evaluated from the Euler-Lagrange equations
for the motion of a massless particle in the background given by 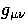 [6,8,9]:
[6,8,9]:
| ![\begin{displaymath}
\vec{G}[h_{\mu\nu}] = \left({1 \over 2}
{n}^i {n}^j \dot h_...
... h_{0i}
+ {1 \over 2} n^i h_{00\vert i} \,, 0 \, , 0 \right) .\end{displaymath}](img58.gif) |
(15) |
Note gravitational redshift affects different polarization states alike.
As should be expected, the modification from the flat space case involves the
replacement of ordinary spatial derivatives with covariant ones.
The Compton scattering term 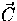 was derived in [1,4]
in the total angular momentum language.
Though the basic result has long been known [10,11], this
representation has the virtue of explicitly showing that complications due
to the angular and polarization dependence of Compton scattering come simply
through the quadrupole moments of the distribution. Here
was derived in [1,4]
in the total angular momentum language.
Though the basic result has long been known [10,11], this
representation has the virtue of explicitly showing that complications due
to the angular and polarization dependence of Compton scattering come simply
through the quadrupole moments of the distribution. Here
| ![\begin{displaymath}
\begin{array}
{rcl}\vec{C}[{\vec {T}}] &=& -\dot\tau
\left...
...\bf P}^{(m)}(\hat{n},\hat{n}') \vec{T}(\hat{n}')\, ,\end{array}\end{displaymath}](img59.gif) |
(16) |
where the differential cross section for Compton scattering is
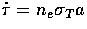 where ne is the free electron number density
and
where ne is the free electron number density
and 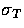 is the Thomson cross section.
The bracketted term in the collision integral describes the isotropization of
the photons in the rest frame of the electons.
The last term accounts for the angular and polarization dependence of the
scattering with
is the Thomson cross section.
The bracketted term in the collision integral describes the isotropization of
the photons in the rest frame of the electons.
The last term accounts for the angular and polarization dependence of the
scattering with
| 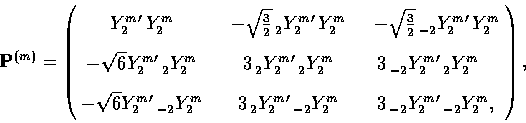 |
(17) |
where 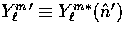 and
and
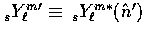 and the unprimed
harmonics have argument
and the unprimed
harmonics have argument 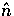 .Here
.Here 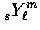 are the spin-weighted spherical harmonics
[12,13,14,1].
are the spin-weighted spherical harmonics
[12,13,14,1].




Next: Normal Modes
Up: Boltzmann Equation
Previous: Boltzmann Equation
Wayne Hu
9/9/1997
![]() is easily evaluated from the Euler-Lagrange equations
for the motion of a massless particle in the background given by
is easily evaluated from the Euler-Lagrange equations
for the motion of a massless particle in the background given by ![]() [6,8,9]:
[6,8,9]:
![]() was derived in [1,4]
in the total angular momentum language.
Though the basic result has long been known [10,11], this
representation has the virtue of explicitly showing that complications due
to the angular and polarization dependence of Compton scattering come simply
through the quadrupole moments of the distribution. Here
was derived in [1,4]
in the total angular momentum language.
Though the basic result has long been known [10,11], this
representation has the virtue of explicitly showing that complications due
to the angular and polarization dependence of Compton scattering come simply
through the quadrupole moments of the distribution. Here