Figures 1-3
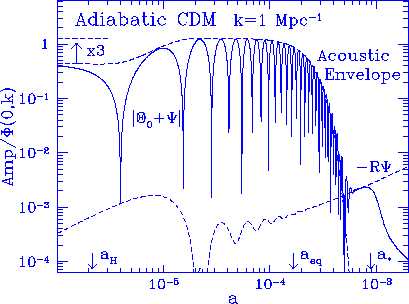 Figure 1
Acoustic oscillations receive a
boost at horizon crossing $a_H$ due driving from gravitational
potential decay.
The perturbations then settle into a pure acoustic mode and are
subsequently damped
by photon diffusion.
Together the potential driving and diffusion damping effects form the
acoustic envelope. After diffusion damping has destroyed the acoustic
oscillations, the underlying baryon drag effect becomes apparent.
Since $\Psi$ is here constant for $a \gg a_{eq}$, $|R\Psi|$ increases
with time.
This contribution itself is damped at last scattering $a_*$ by
cancellation.
Well after last scattering $a \gg a_*$, isotropic perturbations
collisionlessly damp creating angular fluctuations in the CMB.
The model here is adiabatic CDM, $\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$.
Figure 1
Acoustic oscillations receive a
boost at horizon crossing $a_H$ due driving from gravitational
potential decay.
The perturbations then settle into a pure acoustic mode and are
subsequently damped
by photon diffusion.
Together the potential driving and diffusion damping effects form the
acoustic envelope. After diffusion damping has destroyed the acoustic
oscillations, the underlying baryon drag effect becomes apparent.
Since $\Psi$ is here constant for $a \gg a_{eq}$, $|R\Psi|$ increases
with time.
This contribution itself is damped at last scattering $a_*$ by
cancellation.
Well after last scattering $a \gg a_*$, isotropic perturbations
collisionlessly damp creating angular fluctuations in the CMB.
The model here is adiabatic CDM, $\Omega_0=1$, $h=0.5$, $\Omega_b=0.05$.
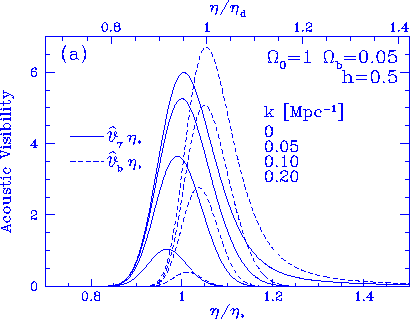
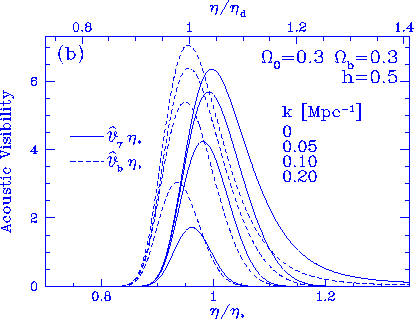 Figure 2
Visibility functions for the photons and baryons.
In the undamped $k\rightarrow 0$ limit, the photon acoustic
visibility and the Compton visibility
are equivalent $\hat \Vg = \Vg$ and the baryon acoustic visibility
equals the drag visibility, $\hat\Vb = \Vb$.
If $\Omega_b h^2 \simlt 0.03$, $\Vb$ peaks at later
times than $\Vg$, \ie\ $\eta_d > \eta_*$.
For small scales, the acoustic visibilities, which weight the
acoustic contributions from the tight coupling regime, are increasingly
suppressed at later times by damping
and the width and amplitude of the acoustic visibilities
decrease as $k$ increases.
Figure 2
Visibility functions for the photons and baryons.
In the undamped $k\rightarrow 0$ limit, the photon acoustic
visibility and the Compton visibility
are equivalent $\hat \Vg = \Vg$ and the baryon acoustic visibility
equals the drag visibility, $\hat\Vb = \Vb$.
If $\Omega_b h^2 \simlt 0.03$, $\Vb$ peaks at later
times than $\Vg$, \ie\ $\eta_d > \eta_*$.
For small scales, the acoustic visibilities, which weight the
acoustic contributions from the tight coupling regime, are increasingly
suppressed at later times by damping
and the width and amplitude of the acoustic visibilities
decrease as $k$ increases.
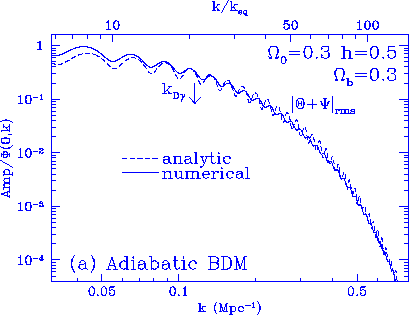

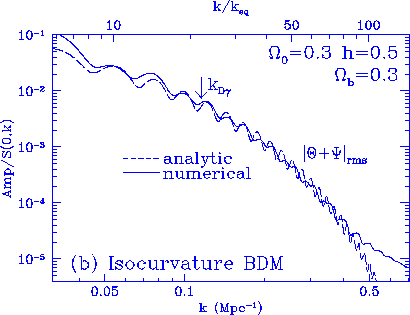
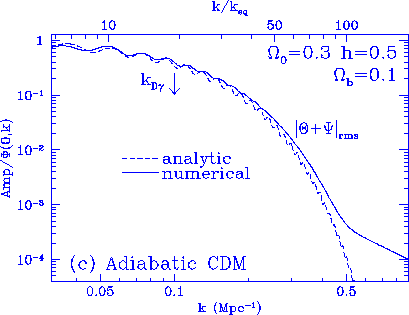 Figure 3
Photon transfer function. Plotted is the present rms photon temperature
fluctuation relative to the initial curvature fluctuation $\Phi(0,k)$ for
adiabatic fluctuations and the initial entropy fluctuation $S(0,k)$ for
isocurvature fluctuations assuming standard recombination.
The intrinsic acoustic amplitude
is approximated by the analysis in Appendix B for scales well inside
the horizon at equality $k \gg k_{eq}$.
The damping is well approximated by the tight coupling
expansion for high $\Omega_b h^2$ and is slightly overestimated for low
values. Below the damping tail, the baryon drag offset clearly
appears in (b) and (c) where
the gravitational potential is not dominated by acoustic density
fluctuations.
An analytic treatment of this effect is given in Appendix A and C.
Figure 3
Photon transfer function. Plotted is the present rms photon temperature
fluctuation relative to the initial curvature fluctuation $\Phi(0,k)$ for
adiabatic fluctuations and the initial entropy fluctuation $S(0,k)$ for
isocurvature fluctuations assuming standard recombination.
The intrinsic acoustic amplitude
is approximated by the analysis in Appendix B for scales well inside
the horizon at equality $k \gg k_{eq}$.
The damping is well approximated by the tight coupling
expansion for high $\Omega_b h^2$ and is slightly overestimated for low
values. Below the damping tail, the baryon drag offset clearly
appears in (b) and (c) where
the gravitational potential is not dominated by acoustic density
fluctuations.
An analytic treatment of this effect is given in Appendix A and C.
 Figure 1
Figure 1
 Figure 1
Figure 1

 Figure 2
Figure 2



 Figure 3
Figure 3