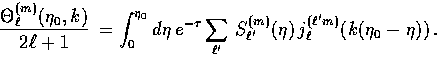
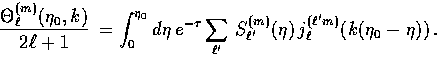 |
(61) |
| (62) |
Similarly, the polarization solutions follow from the radial decomposition of the
| (63) |
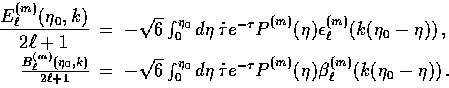 |
Thus the structures of ![]() ,
, ![]() ,and
,and ![]() shown in Figs. 3
and 4 directly reflects the angular power of
the sources
shown in Figs. 3
and 4 directly reflects the angular power of
the sources ![]() and P(m).
There are several general results that can be read off the
radial functions.
Regardless of the source behavior in k, the
B-parity polarization for scalars vanishes, dominates
by a factor of 6 over the electric parity at
and P(m).
There are several general results that can be read off the
radial functions.
Regardless of the source behavior in k, the
B-parity polarization for scalars vanishes, dominates
by a factor of 6 over the electric parity at ![]() for the vectors, and is reduced by a factor of 8/13
for the tensors at
for the vectors, and is reduced by a factor of 8/13
for the tensors at ![]() [see Eqn. (23)].
[see Eqn. (23)].
Furthermore,
the power spectra in ![]() can rise no faster than
can rise no faster than
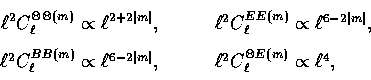 |
Features in k-space
in the ![]() moment at fixed time
are increasingly well preserved in
moment at fixed time
are increasingly well preserved in
![]() -space as |m| increases,
but may be washed out if the source is not
well localized in time. Only sources involving the
visibility function
-space as |m| increases,
but may be washed out if the source is not
well localized in time. Only sources involving the
visibility function ![]() are required to be
well localized at last scattering. However even features
in such sources will be washed out if they occur
in the
are required to be
well localized at last scattering. However even features
in such sources will be washed out if they occur
in the ![]() moment, such as the scalar dipole and the vector
quadrupole (see Fig. 3).
Similarly
features in the vector E and tensor B modes are washed out.
moment, such as the scalar dipole and the vector
quadrupole (see Fig. 3).
Similarly
features in the vector E and tensor B modes are washed out.
The geometric properties of the temperature-polarization cross
power spectrum ![]() can also be read off the integral
solutions. It is first instructive however to rewrite
the integral solutions as
can also be read off the integral
solutions. It is first instructive however to rewrite
the integral solutions as ![]()
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}{\Theta_\ell^{(0)}(\eta_0,...
...eft[ \dot\tau P^{(2)}- \dot H \right] j_\ell^{(22)},\end{array}\end{displaymath}](img298.gif) |
The cross power spectrum contains two pieces: the relation between
the temperature and polarization sources ![]() and
P(m) respectively and the differences in
their projection as anisotropies on the sky. The latter is
independent of the model and provides interesting consequences
in conjunction with tight coupling and
causal constraints on the sources.
In particular, the sign of the correlation is determined by
[21]
and
P(m) respectively and the differences in
their projection as anisotropies on the sky. The latter is
independent of the model and provides interesting consequences
in conjunction with tight coupling and
causal constraints on the sources.
In particular, the sign of the correlation is determined by
[21]
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}{\rm sgn}[C_\ell^{\Theta E...
...}
{\rm sgn}[P^{(2)}(\dot\tau P^{(2)} - \dot H)] \, ,\end{array}\end{displaymath}](img305.gif) |
These integral solutions are also useful in calculations. For example, they may be employed with approximate solutions to the sources in the tight coupling regime to gain physical insight on anisotropy formation (see §IV and [22,23]). Seljak & Zaldarriaga [24] have obtained exact solutions through numerically tracking the evolution of the source by solving the truncated Boltzmann hierarchy equations. Our expression agree with [3,4,24] where they overlap.