Spatial Curvature

Key Concepts:

With the beautiful agreement between the predications and observations of the shape of the first peak, we can now draw inferences from its angular position at l~200 based on the interpretation that we are seeing the first compression of a sound wave before recombination.

The key is that we know the physical scale associated with the peak: the distance sound can travel before recombination, the so-called sound horizon.  We measure the angular scale from the experiments themselves.  Combining the two tells us the spatial curvature of the universe.   Cosmologists call this an angular diameter distance test for curvature.

Let's see how that works.  Think of the more familiar curvautre of the surface of the Earth and imagine you are the observer at the pole.  As you look out at a fixed angle, you are looking along lines of constant longitude.  Since the surface curves, the distance between the two lines is smaller than it would be if the Earth were flat:

In a closed universe, when you look out at a fixed angular scale you are therefore looking at a smaller physical scale.  Conversely, for a fixed physical scale, in our case the distance sound can travel, you have to look out at a larger angle (or lower multipole l) to see its full extent.

The spatial curvature of the universe is related to the total energy density of all consituents of the universe.  You can alternately think of what is doing the curving of the paths of the CMB photons from recombination as gravitational lensing from the intervening energy density.   The upshot is that if the universe is flat, it has a very special energy density called the critical energy density.

Caveats:

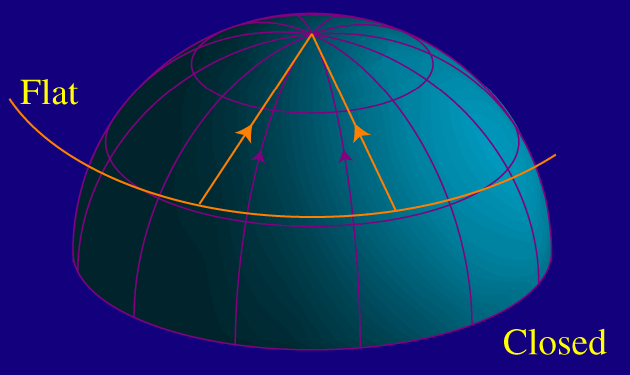
The alert reader will note that this argument shoves one thing under the rug.  The usual use of comparing physical to angular size is to measure the distance to an object.  Think about how you might judge the distance to an on coming car at night.  You look at how far in angle the headlights are separated and knowing how wide a car typically is, you intuitively infer its distance.  You would be thought strange if hypothesized a giant magnifying lens in between making the headlight separation look larger!  So how is that we measure mainly the curvature of the universe and not the distance to recombination?  Fortunately for us, the ambiguities in the distance scale out since they change the distance sound can travel before recombination and the distance CMB light can travel after recombination in the same way.   That's just like redefining what you mean by a meter and doesn't affect angular scales at all.  The residual effects are small as we shall see later but are currently a subject of great interest.

Finally, you should be aware that there is a difference between spatial curvature and curvature of space-time.  Even if space is flat, that the universe is expanding at all is evidence that Einstein was right about space-time being curved!