• Introduction
• Temperature Maps
  • Earth
  • Monopole
  • Dipole
  • COBE
  • Power
  • Precision
  • Features
• Thermal History
  • Expansion
  • Plasma
  • Glue
  • Pressure
  • Thermal
• Acoustic Oscillations
  • Gravity
  • Plane Waves
  • Harmonics
  • Extrema
• Angular Peaks
  • Spatial/Angular
  • Oscillation
  • Freeze Frame
  • Streaming
  • Soundscape
• First Peak
  • Data
  • Curvature
  • Flatness
  • Dark Energy
  • Summary
• Second Peak
  • Data
  • Inertia
  • Baryonmeter
  • Power
  • Dark Baryons
  • Summary
• Higher Peaks
  • Driving Force
  • Power
  • Summary
• Damping Tail
  • Diffusion
  • Ruler
  • Consistency
  • Summary
• Parameter Estimation
  • Parameters
  • Degeneracy
• Polarization
  • What and Why
  • Scattering
  • Projection
  • Power
  • Quadrupoles
  • B-modes
  • Gravity Waves
• Summary

Spatial Curvature

Key Concepts

• Position of peaks mainly sensitive to curvature
• Shapes fixed by the physical density of matter and baryons
• Missing or "dark energy" plays a small roll in the position of peaks

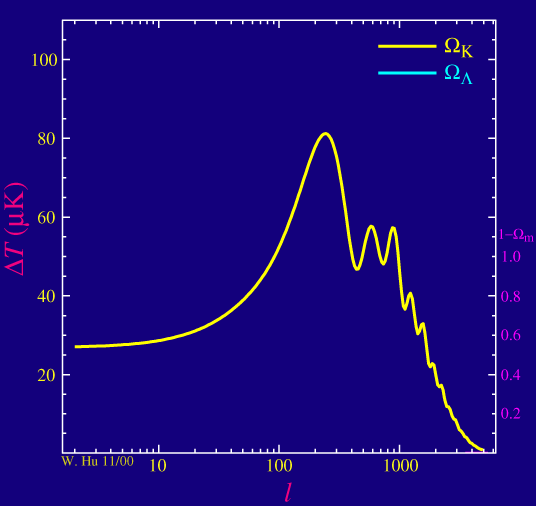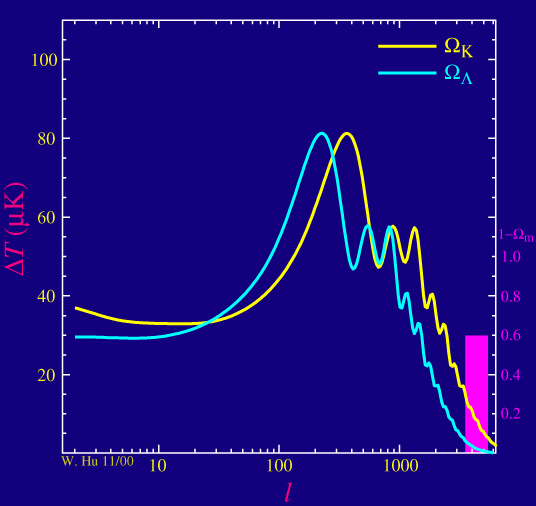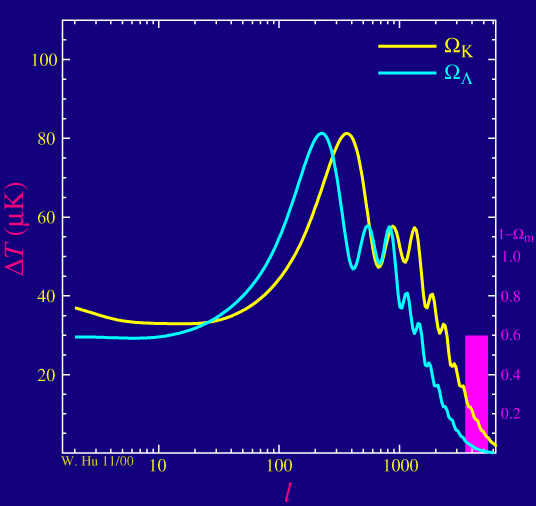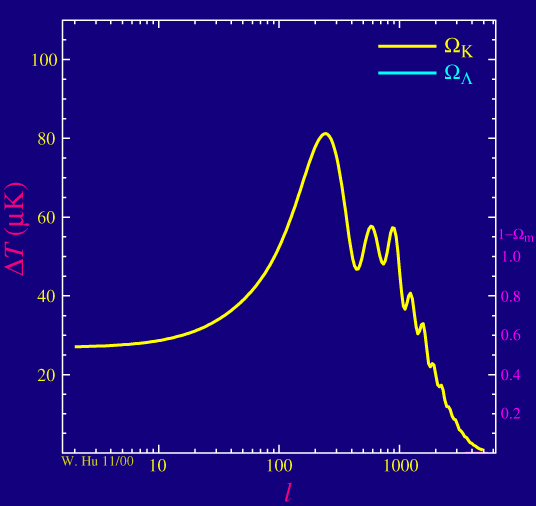
As advertised, the position of that first peak in the power spectrum of the anisotropies, and indeed all of the peaks, depend sensitively on the spatial curvature of the universe.   As the curvature of the universe decreases (and in fact becomes negative in the yellow curve below)

the peaks move to smaller angles (higher multipole l) while preserving their shape.  Cosmologists fraction of the critical density in matter &Omega_m so that as 1-&Omega_mincreases from zero, the universe becomes increasingly negatively curved if there is no other forms of "missing energy" that we've missed in our accounting.

Caveats:

In the blue curve, we assume that there is indeed a form of "missing" or dark energy in a cosmological constant that makes the universe flat despite a sub-critical density of matter.  We see that the positions mainly care about the curvature of the universe but there is a small shift to larger angular scales (lower multipoles) through the introduction of a cosmological constant.  This is because the cosmological constant produces a small change in the distance light can travel since recombination, a fact that is related to its well known effect on the age of the universe.

Note that in the above figure we assume that the physical density of the matter (&Omega_mh²) is fixed.  This is different from saying its fraction of the critical density (&Omega_m) is fixed since the Hubble constant (h), or expansion rate today, enters into the definition of the critical density.  Given our current uncertainties about the physical density of the matter, the distance that sound can travel by recombination is currently uncertain, a fact related to the matter's effect on the age of the universe at recombination.  Likewise we have assumed that the physical density of the baryons  (&Omega_bh²) is fixed.  Baryons lower the speed of sound in the medium and hence also affect the distance sound can travel.  Luckily both of these quantities dramatically change the shape of the peaks as we shall see.  They will be measured once the higher peaks are detected and will no longer confuse the measurement of the curvature.   As it turns out, the sound horizon is not a standard ruler but rather a standardizeable ruler.