



Next: Scalar Einstein Equations
Up: Evolution Equations
Previous: Free Streaming
The explicit form of the
Boltzmann equations for the temperature and polarization
follows directly from the Clebsch-Gordan relation of
Eqn. (58).
For the temperature (s=0),
| 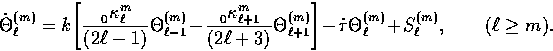 |
(52) |
The term in the square brackets is the free streaming effect
that couples the 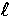 -modes and tells us that in the absence of
scattering power is transferred down the hierarchy when
-modes and tells us that in the absence of
scattering power is transferred down the hierarchy when 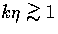 . This transferral merely represents geometrical
projection of fluctuations on the scale corresponding to k at
distance
. This transferral merely represents geometrical
projection of fluctuations on the scale corresponding to k at
distance 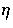 which subtends an angle given by
which subtends an angle given by 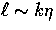 .
The main effect of scattering
comes through the
.
The main effect of scattering
comes through the 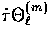 term and implies
an exponential suppression of anisotropies with optical depth in
the absence of sources. The source
term and implies
an exponential suppression of anisotropies with optical depth in
the absence of sources. The source 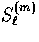 accounts for
the gravitational and residual scattering effects,
accounts for
the gravitational and residual scattering effects,
| 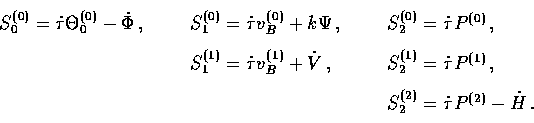 |
(53) |
The presence of 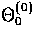 represents the fact that
an isotropic temperature fluctuation is not destroyed by
scattering. The Doppler effect enters the dipole
represents the fact that
an isotropic temperature fluctuation is not destroyed by
scattering. The Doppler effect enters the dipole 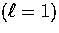 equation through the baryon velocity
vB(m) term. Finally the anisotropic
nature of Compton scattering is expressed through
equation through the baryon velocity
vB(m) term. Finally the anisotropic
nature of Compton scattering is expressed through
| ![\begin{displaymath}
P^{(m)} = {1 \over 10} \left[ \Theta_2^{(m)} -
\sqrt{6} E_2^{(m)} \right],\end{displaymath}](img251.gif) |
(54) |
and involves the quadrupole moments of the temperature and
E-polarization
distribution only.
The polarization evolution follows a similar pattern for
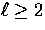 ,
, 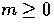 from Eqn. (58) with
from Eqn. (58) with
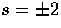 ,
,![[*]](foot_motif.gif)
| ![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}\dot E_\ell^{(m)} &=&
k ...
... B_{\ell + 1}^{(m)}
\Bigg] - \dot\tau B_\ell^{(m)} .\end{array}\end{displaymath}](img256.gif) |
(55) |
Notice that the source of polarization P(m)
enters only in the E-mode quadrupole
due to the opposite parity of 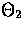 and B2. However, as discussed in §IIB, free
streaming or projection couples the two parities except for
the m=0 scalars. Thus
and B2. However, as discussed in §IIB, free
streaming or projection couples the two parities except for
the m=0 scalars. Thus 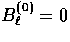 by geometry
regardless of the source.
It is unnecessary to solve separately for the m=-|m| relations
since they satisfy the same equations and solutions with
by geometry
regardless of the source.
It is unnecessary to solve separately for the m=-|m| relations
since they satisfy the same equations and solutions with
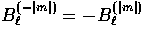 and all other quantities
equal.
and all other quantities
equal.
To complete these equations, we need to express the evolution of
the metric sources 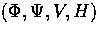 . It is to this subject we
now turn.
. It is to this subject we
now turn.




Next: Scalar Einstein Equations
Up: Evolution Equations
Previous: Free Streaming
Wayne Hu
9/9/1997
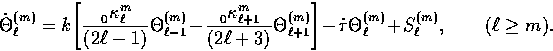
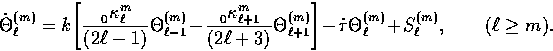
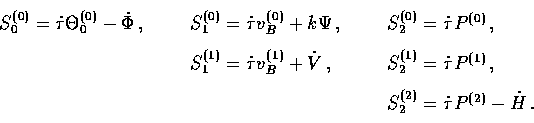
![]() ,
, ![]() from Eqn. (58) with
from Eqn. (58) with
![]() ,
,![[*]](foot_motif.gif)
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}\dot E_\ell^{(m)} &=&
k ...
... B_{\ell + 1}^{(m)}
\Bigg] - \dot\tau B_\ell^{(m)} .\end{array}\end{displaymath}](img256.gif)
![]() . It is to this subject we
now turn.
. It is to this subject we
now turn.