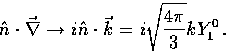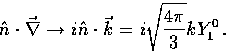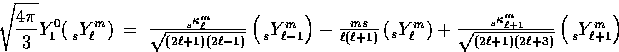Next: Boltzmann Equations
Up: Evolution Equations
Previous: Angular Moments and Power
As the radiation free streams, gradients in the distribution
produce anisotropies. For example, as photons from different
temperature regions intersect on their trajectories, the temperature
difference is reflected in the angular distribution.
This effect is represented in the Boltzmann equation
(45) gradient term,
| 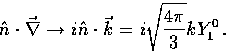 |
(49) |
which multiplies the intrinsic angular dependence of the
temperature and polarization distributions,
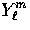 and
and 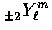 respectively,
from the expansion Eqn. (55) and
the angular basis of Eqns. (10)
and (11). Free streaming
thus involves the
Clebsch-Gordan relation of Eqn. (8)
respectively,
from the expansion Eqn. (55) and
the angular basis of Eqns. (10)
and (11). Free streaming
thus involves the
Clebsch-Gordan relation of Eqn. (8)
| 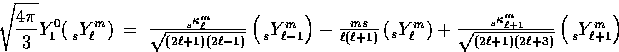 |
(50) |
which couples the 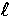 to
to 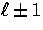 moments of the distribution.
Here the coupling coefficient is
moments of the distribution.
Here the coupling coefficient is
| 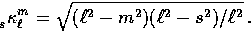 |
(51) |
As we shall now see, the result of this streaming effect is
an infinite hierarchy of coupled 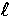 -moments
that passes power from sources at low multipoles up
the
-moments
that passes power from sources at low multipoles up
the 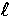 -chain as time progresses.
-chain as time progresses.
Wayne Hu
9/9/1997