

Next: Tensor Einstein Equations
Up: Evolution Equations
Previous: Scalar Einstein Equations
The vector metric source evolution is similarly constructed from
a ``Poisson'' equation
| 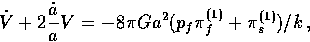 |
(58) |
and the momentum conservation equation for
the stress-energy tensor or Euler equation
where recall 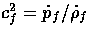 is the sound speed.
Again, the first of these equations remains true for each fluid
individually save for momentum exchange terms.
For the photons
is the sound speed.
Again, the first of these equations remains true for each fluid
individually save for momentum exchange terms.
For the photons 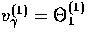 and
and
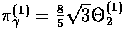 .Thus with the photon Euler equation
(60) (with
.Thus with the photon Euler equation
(60) (with 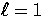 , m=1),
the full baryon equation becomes
, m=1),
the full baryon equation becomes
| 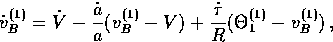 |
(59) |
see Eqn. (67) for details.
Wayne Hu
9/9/1997