



Next: References
Up: A COMPLETE TREATMENT OF
Previous: Radial Functions
We would like to describe the spatial and angular dependence of the normal
modes 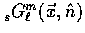 in a coordinate-free way by
constructing them out of covariant derivatives of
in a coordinate-free way by
constructing them out of covariant derivatives of 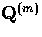 contracted
with some orthonormal basis
contracted
with some orthonormal basis 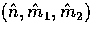 .The lowest
.The lowest  modes can be written as
[3,4],
and satisfy (Appendix B),
modes can be written as
[3,4],
and satisfy (Appendix B),
| ![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(\vec{x},\hat{n}) =
(-...
...om{m}} Y_{\ell}^{m}(\hat{n})] \exp[i\delta(\vec{x},\vec{k})]\,,\end{displaymath}](img212.gif) |
(55) |
with 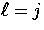 . We demand that the higher
. We demand that the higher 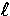 -modes also do so,
to maintain the division of spin and orbital angular momentum defined in
flat space [1].
-modes also do so,
to maintain the division of spin and orbital angular momentum defined in
flat space [1].
We begin the construction by choosing some arbitrary point 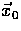 ,and using a spherical coordinate system around it,
,and using a spherical coordinate system around it,
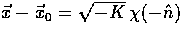 .Now
.Now 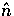 defines both the intrinsic angular coordinate system and
the angular coordinates for the spatial location
defines both the intrinsic angular coordinate system and
the angular coordinates for the spatial location 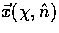 .This reduction in the dimension of the space is sufficient since the
end goal is to derive how the intrinsic and orbital angular dependence
in the same direction
.This reduction in the dimension of the space is sufficient since the
end goal is to derive how the intrinsic and orbital angular dependence
in the same direction 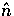 adds. In physical terms, only those
photons directed toward the observer can contribute to the local
angular dependence there.
First expand the lowest mode in spin-spherical harmonics
adds. In physical terms, only those
photons directed toward the observer can contribute to the local
angular dependence there.
First expand the lowest mode in spin-spherical harmonics
| 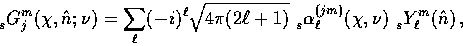 |
(56) |
where recall that the dimensionless wavenumber is 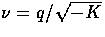 .We obtain the explicit expressions for
.We obtain the explicit expressions for 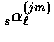 and their recursion relations
in Appendix B by simple comparison between equations
(C1)
and (C3). At the origin they satisfy
and their recursion relations
in Appendix B by simple comparison between equations
(C1)
and (C3). At the origin they satisfy
| 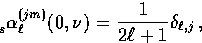 |
(57) |
which both fixes the normalization of the modes and manifestly obeys
Eq. (C2).
As 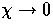 only the local angular dependence remains, as
expressed in the Kronecker delta of Eq. (C4).
Because the spatial variation of the normal mode Q(m) across a shell
at fixed radius
only the local angular dependence remains, as
expressed in the Kronecker delta of Eq. (C4).
Because the spatial variation of the normal mode Q(m) across a shell
at fixed radius 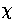 must be added to the local dependence, even a mode
of fixed j has a sum over all
must be added to the local dependence, even a mode
of fixed j has a sum over all 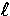 in its angular dependence which
contributes at any other point.
in its angular dependence which
contributes at any other point.
This generation of higher 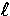 structure as
structure as 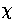 increases suggests that
we can use the radial structure of
increases suggests that
we can use the radial structure of 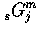 to generate the higher
to generate the higher
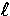 modes.
From the radial recursion relation for
modes.
From the radial recursion relation for 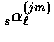 Eq. (B9), let us make the ansatz
Eq. (B9), let us make the ansatz
| 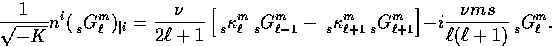 |
(58) |
That this series generates modes with the desired properties can be shown
by returning to the spherical coordinate system.
By explicit substitution of the radial form for
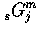 of Eq. (C3)
and by noting that in this coordinate system
of Eq. (C3)
and by noting that in this coordinate system
| 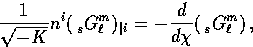 |
(59) |
we obtain
| ![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(0,\hat{n}) =
(-i)^\el...
...2\ell+1}}
[\, {}_{s}^{\vphantom{m}} Y_{\ell}^{m}(\hat{n})] \,,\end{displaymath}](img221.gif) |
(60) |
(up to a phase factor) as desired.
Since we have shown this for an arbitrary point, it is clear that
Eq. (C2) holds in general.
Note that this construction requires
| 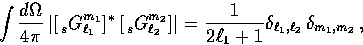 |
(61) |
for all 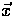 , as in the flat case of Eq. (24), and defines
our normalization convention.
, as in the flat case of Eq. (24), and defines
our normalization convention.




Next: References
Up: A COMPLETE TREATMENT OF
Previous: Radial Functions
Wayne Hu
9/9/1997
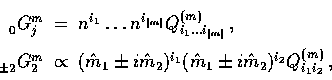
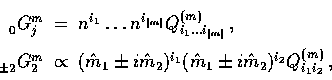
![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(\vec{x},\hat{n}) =
(-...
...om{m}} Y_{\ell}^{m}(\hat{n})] \exp[i\delta(\vec{x},\vec{k})]\,,\end{displaymath}](img212.gif)
![]() ,and using a spherical coordinate system around it,
,and using a spherical coordinate system around it,
![]() .Now
.Now ![]() defines both the intrinsic angular coordinate system and
the angular coordinates for the spatial location
defines both the intrinsic angular coordinate system and
the angular coordinates for the spatial location ![]() .This reduction in the dimension of the space is sufficient since the
end goal is to derive how the intrinsic and orbital angular dependence
in the same direction
.This reduction in the dimension of the space is sufficient since the
end goal is to derive how the intrinsic and orbital angular dependence
in the same direction ![]() adds. In physical terms, only those
photons directed toward the observer can contribute to the local
angular dependence there.
First expand the lowest mode in spin-spherical harmonics
adds. In physical terms, only those
photons directed toward the observer can contribute to the local
angular dependence there.
First expand the lowest mode in spin-spherical harmonics
![]() structure as
structure as ![]() increases suggests that
we can use the radial structure of
increases suggests that
we can use the radial structure of ![]() to generate the higher
to generate the higher
![]() modes.
From the radial recursion relation for
modes.
From the radial recursion relation for ![]() Eq. (B9), let us make the ansatz
Eq. (B9), let us make the ansatz
![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(0,\hat{n}) =
(-i)^\el...
...2\ell+1}}
[\, {}_{s}^{\vphantom{m}} Y_{\ell}^{m}(\hat{n})] \,,\end{displaymath}](img221.gif)