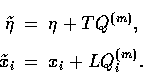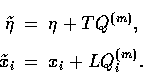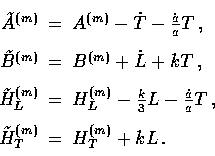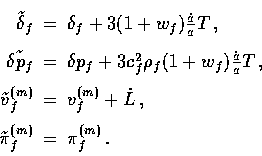Next: Scalar Einstein Equations
Up: Einstein Equations
Previous: Background Evolution
To represent the perturbations we must make a gauge choice.
A gauge transformation is a change in the correspondence between the
perturbation and the background represented by the coordinate shifts
T corresponds to a choice in time slicing and L a choice of
spatial coordinates. Since scalar and vector quantities
cannot be formed from tensor modes (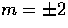 ),
no gauge freedom remains there. Under the condition that
metric distances be invariant,
they transform the metric as [17]
The stress-energy perturbations in different gauges are similarly
related by the gauge transformations
Note that the anisotropic stress is gauge-invariant.
Seed perturbations are also gauge-invariant to lowest order, whereas
a scalar field transforms as
),
no gauge freedom remains there. Under the condition that
metric distances be invariant,
they transform the metric as [17]
The stress-energy perturbations in different gauges are similarly
related by the gauge transformations
Note that the anisotropic stress is gauge-invariant.
Seed perturbations are also gauge-invariant to lowest order, whereas
a scalar field transforms as
| 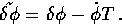 |
(37) |
The relation between the synchronous and Newtonian gauge equations follow
from these relations.
Wayne Hu
9/9/1997