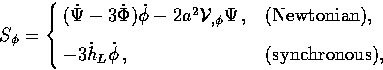Next: Vector Einstein Equations
Up: Einstein Equations
Previous: Gauge Transformations
With the form of the scalar metric and stress energy tensor given
in Eqs. (A4) and (15), the ``Poisson''
equations become in the Newtonian gauge
| 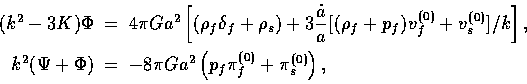 |
(38) |
and in the synchronous gauge
Two out of four of the synchronous gauge equations are redundant.
The corresponding evolution of the matter is given by covariant conservation
of the stress energy tensor 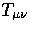 :
:
for the fluid part. The gravitational sources are
| 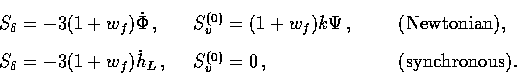 |
(39) |
These equations remain true for each fluid individually in the absence
of momentum exchange, e.g. for the cold dark matter.
The baryons have an additional term to the Euler equation due to momentum
exchange from Compton scattering with the photons.
For a given velocity perturbation the momentum density ratio between the two
fluids is
| 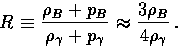 |
(40) |
A comparison with photon Euler equation (33; 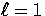 ) gives
the source modification for the baryon Euler equation
) gives
the source modification for the baryon Euler equation
| 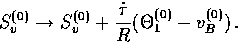 |
(41) |
For a seed source, the conservation equations become
independent of gauge since the metric fluctuations produce higher order terms.
Finally for a scalar field, 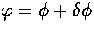 , the conservation
equations become
, the conservation
equations become
| 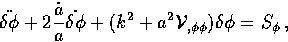 |
(42) |
where
| 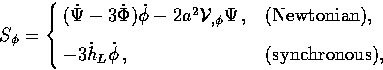 |
(43) |
are the gravitational sources.




Next: Vector Einstein Equations
Up: Einstein Equations
Previous: Gauge Transformations
Wayne Hu
9/9/1997
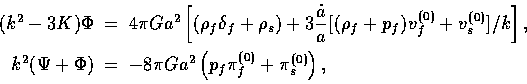
![\begin{displaymath}
\begin{array}
{rcl}(k^2 - 3K)(h_L + {1 \over 3} h_T) + 3{\do...
...T) &=&
-8\pi Ga^2 [p_f \pi_f^{(0)}+ \pi_s^{(0)}]\,.\end{array}\end{displaymath}](img167.gif)
![]() :
:
![\begin{displaymath}
\begin{array}
{rcl}\dot \delta_f
& = & -(1+w_f)kv_f^{(0)}- 3...
...over 3}(1-3K/k^2)\pi_f^{(0)}\right] + S^{(0)}_v \, ,\end{array}\end{displaymath}](img169.gif)
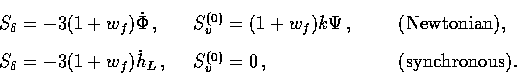
![\begin{displaymath}
\begin{array}
{rcl}\dot \rho_s &=&
-3{\dot a \over a} (\rho...
...[ p_s -{2 \over 3}
(1-3K/k^2)\pi_s^{(0)}\right]\, ,\end{array}\end{displaymath}](img174.gif)
![]() , the conservation
equations become
, the conservation
equations become