



Next: Eigenmodes
Up: A COMPLETE TREATMENT OF
Previous: Introduction
In this section, we discuss the representation of the perturbations for
the cosmological fluids and the geometry of space time.
We start by defining the basis in which we shall expand such perturbations
and their representation under various gauge choices.
We assume that background is described by an FRW metric
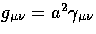 with scale factor a(t) and constant comoving curvature
with scale factor a(t) and constant comoving curvature
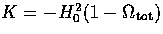 in the spatial metric
in the spatial metric 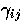 .Here greek indices run from to 3 while latin indices run over the
spatial part of the metric: i,j=1,2,3.
It is often convenient to represent the metric in spherical coordinates where
.Here greek indices run from to 3 while latin indices run over the
spatial part of the metric: i,j=1,2,3.
It is often convenient to represent the metric in spherical coordinates where
| ![\begin{displaymath}
\gamma_{ij} dx^i dx^j = \vert K\vert^{-1} \left[ d\chi^2 + \sin_K^2\chi
( d \theta^2 + \sin^2\theta\, d\phi^2 ) \right]\,, \end{displaymath}](img4.gif) |
(1) |
with
| 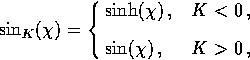 |
(2) |
where the flat-limit expressions are regained as 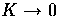 from
above or below. The component corresponding to conformal time
from
above or below. The component corresponding to conformal time
| 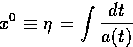 |
(3) |
is 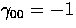 .
.
Small perturbations 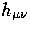 around this FRW metric
around this FRW metric
| 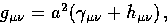 |
(4) |
can be decomposed into
scalar (m=0, compressional),
vector (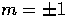 , vortical) and tensor (
, vortical) and tensor (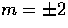 , gravitational wave)
components from their transformation properties under spatial rotations
[6,1].
, gravitational wave)
components from their transformation properties under spatial rotations
[6,1].




Next: Eigenmodes
Up: A COMPLETE TREATMENT OF
Previous: Introduction
Wayne Hu
9/9/1997
![]() with scale factor a(t) and constant comoving curvature
with scale factor a(t) and constant comoving curvature
![]() in the spatial metric
in the spatial metric ![]() .Here greek indices run from to 3 while latin indices run over the
spatial part of the metric: i,j=1,2,3.
It is often convenient to represent the metric in spherical coordinates where
.Here greek indices run from to 3 while latin indices run over the
spatial part of the metric: i,j=1,2,3.
It is often convenient to represent the metric in spherical coordinates where
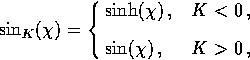
![]() around this FRW metric
around this FRW metric