



Next: Boltzmann Equation
Up: Metric and Stress-Energy Perturbations
Previous: Eigenmodes
A general metric perturbation can be broken up into the normal modes of
scalar (m=0), vector (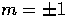 ) and tensor (
) and tensor (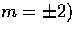 types,
types,
Note that scalar quantities cannot be formed from vector and tensor modes
so that A(m)=0 and HL(m)=0 for 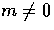 ; likewise vector quantities
cannot be formed from tensor modes so that B(m)=0 for |m| = 2.
; likewise vector quantities
cannot be formed from tensor modes so that B(m)=0 for |m| = 2.
There remains gauge freedom associated with the coordinate
choice for the metric perturbations (see Appendix A2).
It is typically employed to eliminate two out of four of these
quantities for scalar perturbations and one of the two for vector
perturbations. The metric is thus specified by four quantities.
Two popular choices are the synchronous gauge, where
and the generalized (or conformal) Newtonian gauge, where
Here and below, when only the 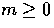 expressions are displayed, the
m < 0 expressions should be taken to be identical unless otherwise
specified.
expressions are displayed, the
m < 0 expressions should be taken to be identical unless otherwise
specified.
The stress energy tensor can likewise be broken up into scalar, vector,
and tensor contributions. Furthermore one can separate fluid (f)
contributions and seed (s) contributions.
The latter is distinguished by the fact that the net effect can be viewed
as a perturbation to the background.
Specifically 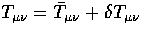 where
where
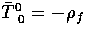 ,
,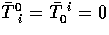 and
and 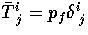 is given by the fluid alone.
The fluctuations can be decomposed into the normal modes of
§IIA as
is given by the fluid alone.
The fluctuations can be decomposed into the normal modes of
§IIA as
| 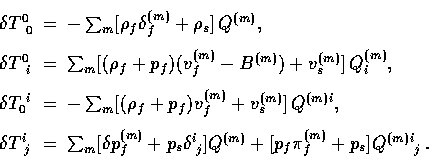 |
(11) |
Since 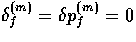 for
for 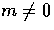 , we hereafter
drop the superscript from these quantities.
, we hereafter
drop the superscript from these quantities.
A minimally coupled scalar field  with Lagrangian
with Lagrangian
| ![\begin{displaymath}
{\cal L} = -{1 \over 2} \sqrt{-g} \left[ g^{\mu \nu} \partial_\mu \varphi
\partial_\nu \varphi + 2V(\varphi) \right]\end{displaymath}](img42.gif) |
(12) |
can be treated in the same way with the associations
| 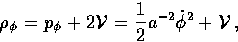 |
(13) |
for the background density and pressure. The fluctuations 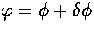 are related to the fluid quantities as [17]
The evolution of the matter and metric perturbations follows from the
Einstein equations
are related to the fluid quantities as [17]
The evolution of the matter and metric perturbations follows from the
Einstein equations 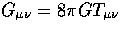 and encorporates
the continuity and Euler equations through the implied energy-momentum
conservation
and encorporates
the continuity and Euler equations through the implied energy-momentum
conservation 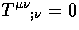 .We give these relations explicitly for the scalar, vector and tensor
perturbations in both Newtonian and synchronous gauge in
Appendix A (see also [7]).
.We give these relations explicitly for the scalar, vector and tensor
perturbations in both Newtonian and synchronous gauge in
Appendix A (see also [7]).
These equations hold equally well for relativistic matter such as the
CMB photons and the neutrinos. However in that case they do not represent
a closed system of equations (the equation of motion of the anisotropic
stress perturbations 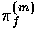 is unspecified) and do not account for
the higher moments of the distribution or for momentum exchange between
different particle species.
To include these effects, we require the Boltzmann equation
which describes the evolution of the full distribution function under
collisional processes.
is unspecified) and do not account for
the higher moments of the distribution or for momentum exchange between
different particle species.
To include these effects, we require the Boltzmann equation
which describes the evolution of the full distribution function under
collisional processes.




Next: Boltzmann Equation
Up: Metric and Stress-Energy Perturbations
Previous: Eigenmodes
Wayne Hu
9/9/1997
![]() ) and tensor (
) and tensor (![]() types,
types,
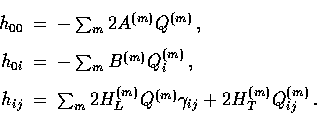
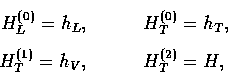
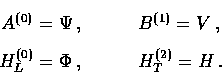
![]() where
where
![]() ,
,![]() and
and ![]() is given by the fluid alone.
The fluctuations can be decomposed into the normal modes of
§IIA as
is given by the fluid alone.
The fluctuations can be decomposed into the normal modes of
§IIA as
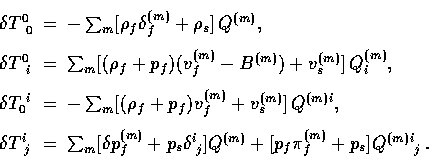
![]() with Lagrangian
with Lagrangian
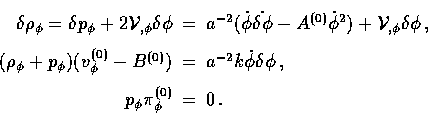
![]() is unspecified) and do not account for
the higher moments of the distribution or for momentum exchange between
different particle species.
To include these effects, we require the Boltzmann equation
which describes the evolution of the full distribution function under
collisional processes.
is unspecified) and do not account for
the higher moments of the distribution or for momentum exchange between
different particle species.
To include these effects, we require the Boltzmann equation
which describes the evolution of the full distribution function under
collisional processes.