



Next: Vector Perturbations
Up: Perturbation Classification
Previous: Perturbation Classification
Scalar perturbations in a flat universe are represented by
plane waves
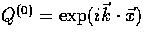 ,which are the eigenfunctions
of the Laplacian operator
,which are the eigenfunctions
of the Laplacian operator
| 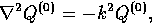 |
(18) |
and their spatial derivatives. For example,
vector and symmetric tensor quantities such as velocities and
stresses based on scalar perturbations
can be constructed as
| ![\begin{displaymath}
Q_i^{(0)}= - k^{-1} \nabla_i Q^{(0)}, \qquad Q_{ij}^{(0)}=
[k^{-2} \nabla_i \nabla_j + {1 \over 3} \delta_{ij}] Q^{(0)}.\end{displaymath}](img130.gif) |
(19) |
Since 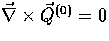 , velocity fields
based on scalar perturbations are irrotational.
Notice that Q(0)= G00, ni Qi(0)= G10 and
, velocity fields
based on scalar perturbations are irrotational.
Notice that Q(0)= G00, ni Qi(0)= G10 and
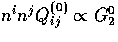 ,where the coordinate system is defined by
,where the coordinate system is defined by 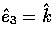 .From the orthogonality of the spherical harmonics, it follows
that scalars generate only m=0 fluctuations in the radiation.
.From the orthogonality of the spherical harmonics, it follows
that scalars generate only m=0 fluctuations in the radiation.
Wayne Hu
9/9/1997
![]() ,which are the eigenfunctions
of the Laplacian operator
,which are the eigenfunctions
of the Laplacian operator