Vector Perturbations

Vector perturbations can be decomposed into harmonic modes 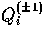$Q^{(\pm 1)}_i$ of the Laplacian in the same manner as the scalars,  

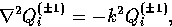$$\nabla^2 Q^{(\pm 1)}_{i} = -k^2 Q^{(\pm 1)}_{i} ,$$ (20)

which satisfy a divergenceless condition

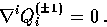$${\nabla}^i {Q}_i^{(\pm 1)}= 0 \, .$$ (21)

A velocity field based on vector perturbations thus represents vorticity, whereas scalar objects such as density perturbations are entirely absent. The corresponding symmetric tensor is constructed out of derivatives as

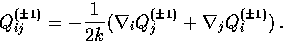$$Q_{ij}^{(\pm 1)}= - {1 \over 2k} (\nabla_i Q_j^{(\pm 1)}+ \nabla_j Q_i^{(\pm 1)})\, .$$ (22)

A convenient representation is

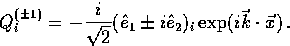$${Q}_i^{(\pm 1)}= - {i \over \sqrt{2}} (\hat{e}_1 \pm i \hat{e}_2)_i \exp(i\vec{k} \cdot \vec{x}) \, .$$ (23)

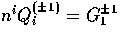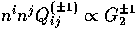Notice that $n^i Q_i^{(\pm 1)}= G_1^{\pm 1}$ and $n^i n^j Q_{ij}^{(\pm 1)}\propto G_2^{\pm 1}$. Thus vector perturbations stimulate the 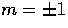$m = \pm 1$ modes in the radiation.