



Next: Scalar Perturbations
Up: Normal Modes
Previous: Interpretation
As is well known (see e.g. [7,15]), a
general symmetric tensor such as the metric and stress-energy
perturbations can be separated into scalar, vector
and tensor pieces through their coordinate transformation
properties. We now review the properties of their
normal modes so that they
may be related to those of the radiation. We find that
the 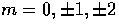 modes of the radiation couple to the
scalar, vector and tensor modes of the metric. Although we
consider flat geometries here, we preserve
a covariant notation that ensures straightforward generalization
to open geometries through the replacement of
modes of the radiation couple to the
scalar, vector and tensor modes of the metric. Although we
consider flat geometries here, we preserve
a covariant notation that ensures straightforward generalization
to open geometries through the replacement of 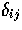 with the curved three metric
and ordinary derivatives with covariant derivatives [6,7].
with the curved three metric
and ordinary derivatives with covariant derivatives [6,7].
Wayne Hu
9/9/1997