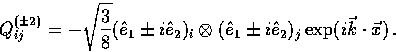Tensor Perturbations

Tensor perturbations are represented by Laplacian eigenfunctions  

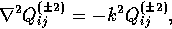$$\nabla^2 Q_{ij}^{(\pm 2)}= -k^2 Q_{ij}^{(\pm 2)},$$ (24)

which satisfy a transverse-traceless condition

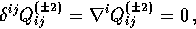$$\delta^{ij} Q^{(\pm 2)}_{ij} = \nabla^i Q^{(\pm 2)}_{ij}{} = 0\, ,$$ (25)

that forbids the construction of scalar and vector objects such as density and velocity fields. The modes take on an explicit representation of

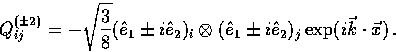$${Q}_{ij}^{(\pm 2)}= - \sqrt{3 \over 8} (\hat{e}_1 \pm i \h... ...at{e}_1 \pm i \hat{e}_2 )_j \exp(i \vec{k} \cdot \vec{x})\, .$$ (26)

Notice that 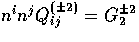$n^i n^j Q_{ij}^{(\pm 2)}= G_2^{\pm 2}$ and thus tensors stimulate the 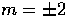$m = \pm 2$ modes in the radiation.

In the following sections, we often only explicitly show the positive m value with the understanding that its opposite takes on the same form except where otherwise noted (i.e. in the B-type polarization where a sign reversal occurs).