



Next: Stress Energy Tensor
Up: Perturbations
Previous: Perturbations
The ultimate source of CMB anisotropies is the gravitational
redshift induced by the metric fluctuation 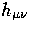
| 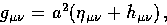 |
(27) |
where the zeroth component represents conformal time
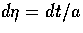 and, in the flat universe considered here,
and, in the flat universe considered here,
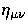 is the Minkowski metric.
The metric perturbation can be further broken up into the
normal modes of
scalar, vector and tensor types as in §IIC.
Scalar and vector modes
exhibit gauge freedom which is fixed by an explicit choice of
the coordinates that relate the perturbation to the background.
For the scalars, we choose the Newtonian gauge (see e.g.
[15,17])
is the Minkowski metric.
The metric perturbation can be further broken up into the
normal modes of
scalar, vector and tensor types as in §IIC.
Scalar and vector modes
exhibit gauge freedom which is fixed by an explicit choice of
the coordinates that relate the perturbation to the background.
For the scalars, we choose the Newtonian gauge (see e.g.
[15,17])
| 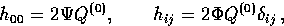 |
(28) |
where the metric is shear free. For the vectors, we choose
and the tensors
Note that tensor fluctuations do not exhibit gauge freedom of
this type.
Wayne Hu
9/9/1997