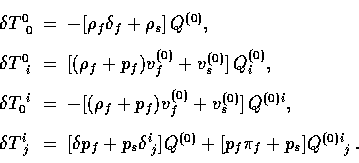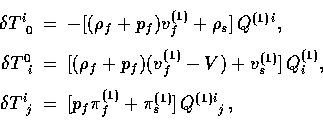


Next: Radiation Transport
Up: Perturbations
Previous: Metric Tensor
The stress energy tensor can be broken up into fluid (f)
contributions
and seed (s) contributions (see e.g. [18]).
The latter is distinguished by the fact
that the net effect can be viewed as a perturbation to the
background. Specifically 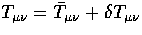 where
where
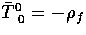 ,
,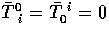 and
and 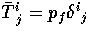 is given by the fluid alone. The fluctuations can be
decomposed into the normal modes of §IIC as
is given by the fluid alone. The fluctuations can be
decomposed into the normal modes of §IIC as
| 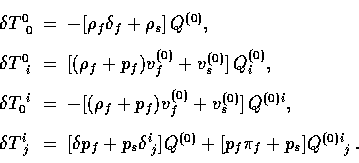 |
(31) |
for the scalar components,
| 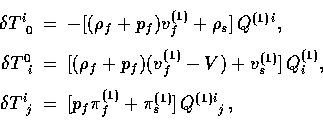 |
(32) |
for the vector components, and
| ![\begin{displaymath}
\delta T^i_{\hphantom{0}j} = [p_f\pi_f^{{(2)}} + \pi_s^{(2)}] \,
Q^{(2)}{}^i_{\hphantom{i}j} \, ,\end{displaymath}](img155.gif) |
(33) |
for the tensor components.
Wayne Hu
9/9/1997
![]() where
where
![]() ,
,![]() and
and ![]() is given by the fluid alone. The fluctuations can be
decomposed into the normal modes of §IIC as
is given by the fluid alone. The fluctuations can be
decomposed into the normal modes of §IIC as