



Next: Evolution Equations
Up: Radiation Transport
Previous: Scattering Matrix
In a perturbed metric, gravitational
interactions alter the temperature perturbation 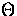 .
The redshift properties may be formally derived by employing the
equation of motion for the photon energy
.
The redshift properties may be formally derived by employing the
equation of motion for the photon energy 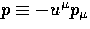 where
where 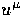 is the 4-velocity of an observer at rest
in the background frame and
is the 4-velocity of an observer at rest
in the background frame and 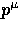 is the photon 4-momentum.
The Euler-Lagrange
equations of motion for the photon and the requirement
that |u2|=1 result in
is the photon 4-momentum.
The Euler-Lagrange
equations of motion for the photon and the requirement
that |u2|=1 result in
| 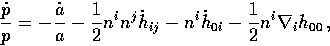 |
(45) |
which differs from [20,7] since we take 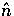 to be the photon propagation direction rather than the viewing
direction of the observer.
The first term is the cosmological reshift due to the expansion
of the spatial metric; it does not affect temperature perturbations
to be the photon propagation direction rather than the viewing
direction of the observer.
The first term is the cosmological reshift due to the expansion
of the spatial metric; it does not affect temperature perturbations
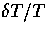 . The second term has a similar origin and is due
to stretching of the spatial metric. The third and fourth term
are the frame dragging and time dilation effects.
. The second term has a similar origin and is due
to stretching of the spatial metric. The third and fourth term
are the frame dragging and time dilation effects.
Since gravitational redshift affects the different polarization
states alike,
| ![\begin{displaymath}
\vec{G}[h_{\mu\nu}] = \left({1 \over 2}
{n}^i {n}^j \dot h_...
..._{0i}
+ {1 \over 2} n^i \nabla_i h_{00} \,, 0 \, , 0 \right) ,\end{displaymath}](img215.gif) |
(46) |
in the 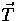 basis.
We now explicitly evaluate the Boltzmann equation for scalar,
vector, and tensor metric fluctuations of
Eqns. (36)-(38).
basis.
We now explicitly evaluate the Boltzmann equation for scalar,
vector, and tensor metric fluctuations of
Eqns. (36)-(38).




Next: Evolution Equations
Up: Radiation Transport
Previous: Scattering Matrix
Wayne Hu
9/9/1997
![]() .
The redshift properties may be formally derived by employing the
equation of motion for the photon energy
.
The redshift properties may be formally derived by employing the
equation of motion for the photon energy ![]() where
where ![]() is the 4-velocity of an observer at rest
in the background frame and
is the 4-velocity of an observer at rest
in the background frame and ![]() is the photon 4-momentum.
The Euler-Lagrange
equations of motion for the photon and the requirement
that |u2|=1 result in
is the photon 4-momentum.
The Euler-Lagrange
equations of motion for the photon and the requirement
that |u2|=1 result in