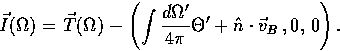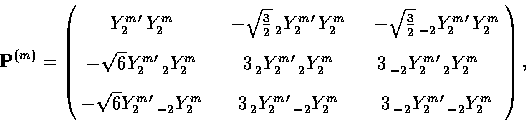Next: Gravitational Redshift
Up: Radiation Transport
Previous: Stokes Parameters
The
calculation of Thomson scattering including polarization was
first performed by Chandrasekhar [16];
here we show a much simpler derivation employing the spin
harmonics.
The Thomson differential scattering cross section
depends on angle as
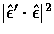 where
where 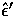 and
and 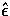 are the incoming and outgoing polarization
vectors respectively in the electron rest frame.
Radiation polarized perpendicular to the
scattering plane scatters isotropically,
while that in the scattering plane
picks up a factor of
are the incoming and outgoing polarization
vectors respectively in the electron rest frame.
Radiation polarized perpendicular to the
scattering plane scatters isotropically,
while that in the scattering plane
picks up a factor of 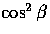 where
where 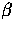 is the scattering
angle.
If the radiation has different intensities or temperatures
at right angles, the radiation scattered into a given angle
will be linearly polarized.
is the scattering
angle.
If the radiation has different intensities or temperatures
at right angles, the radiation scattered into a given angle
will be linearly polarized.
Now let us evaluate the scattering term explicitly.
The angular dependence of the scattering gives
| 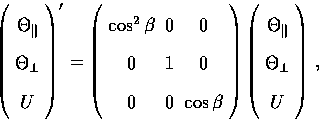 |
(38) |
where the U transformation follows from its definition
in terms of the
difference in intensities polarized 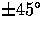 from the
scattering plane.
With the relations
from the
scattering plane.
With the relations 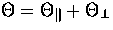 and
and
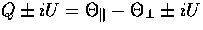 ,
the angular dependence
in the
,
the angular dependence
in the 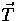 representation of Eqn. (44)
becomes,
representation of Eqn. (44)
becomes,![[*]](foot_motif.gif)
| 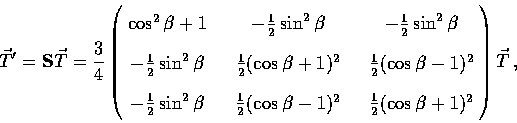 |
(39) |
where the overall normalization is fixed by photon conservation in
the scattering. To relate these scattering frame quantities to those
in the frame defined by 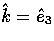 , we must first perform
a rotation from the
, we must first perform
a rotation from the 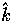 frame to the scattering frame.
The geometry is displayed in Fig. 1, where
the angle
frame to the scattering frame.
The geometry is displayed in Fig. 1, where
the angle 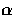 separates the scattering plane from
the meridian plane at
separates the scattering plane from
the meridian plane at 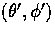 spanned by
spanned by 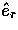 and
and 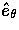 .
After scattering, we rotate by
the angle between the scattering plane and the meridian plane
at
.
After scattering, we rotate by
the angle between the scattering plane and the meridian plane
at 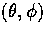 to return to the
to return to the 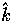 frame.
Eqn. (43) tells us these rotations
transform
frame.
Eqn. (43) tells us these rotations
transform 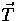 as
as 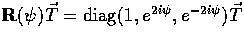 .
The net result is thus expressed as
.
The net result is thus expressed as
| 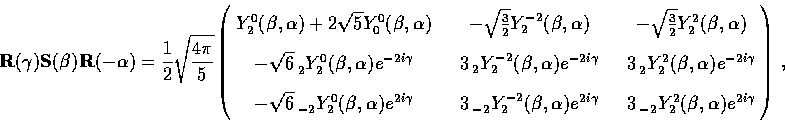 |
(40) |
where we have employed the explict spin-2, 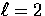 forms in Tab. 1.
Integrating over incoming angles, we obtain the collision term
in the electron rest frame
forms in Tab. 1.
Integrating over incoming angles, we obtain the collision term
in the electron rest frame
| ![\begin{displaymath}
\vec{C}[{\vec {T}}]_{\rm rest}
= -\dot\tau \vec{T}(\Omega) ...
...f R}(\gamma){\bf S}(\beta){\bf R}(-\alpha) \vec{T}(\Omega')\, ,\end{displaymath}](img197.gif) |
(41) |
where the two terms on the rhs
account for scattering out of and into
a given angle respectively. Here the differential optical
depth 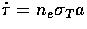 sets the collision rate
in conformal time with ne as the free electron density
and
sets the collision rate
in conformal time with ne as the free electron density
and 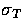 as the Thomson cross section.
as the Thomson cross section.
The transformation from the electron rest frame into the
background frame yields a Doppler shift
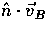 in the temperature of the scattered radiation.
With the help of the generalized addition relation for the harmonics
Eqn. (7), the full collision term can be written
as
in the temperature of the scattered radiation.
With the help of the generalized addition relation for the harmonics
Eqn. (7), the full collision term can be written
as
| ![\begin{displaymath}
\vec{C}[{\vec {T}}] = -\dot\tau {\vec I}(\Omega) +
{1 \ove...
...sum_{m=-2}^2 {\bf P}^{(m)}(\Omega,\Omega') \vec{T}(\Omega')\, .\end{displaymath}](img201.gif) |
(42) |
The vector 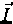 describes
the isotropization of distribution in the
electron rest frame and is given by
describes
the isotropization of distribution in the
electron rest frame and is given by
| 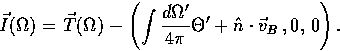 |
(43) |
The matrix 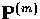 encapsulates the anisotropic nature
of Thomson scattering and shows that as expected
polarization is generated through quadrupole anisotropies
in the temperature and vice versa
encapsulates the anisotropic nature
of Thomson scattering and shows that as expected
polarization is generated through quadrupole anisotropies
in the temperature and vice versa
| 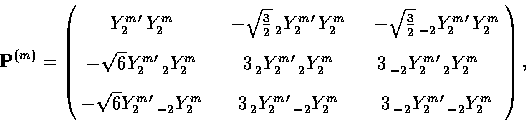 |
(44) |
where 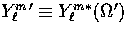 and
and 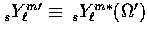 and the unprimed harmonics are with respect to
and the unprimed harmonics are with respect to 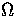 .These
.These 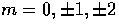 components correspond to the
scalar, vector and tensor scattering terms as discussed in
§IIC and IIIC.
components correspond to the
scalar, vector and tensor scattering terms as discussed in
§IIC and IIIC.




Next: Gravitational Redshift
Up: Radiation Transport
Previous: Stokes Parameters
Wayne Hu
9/9/1997
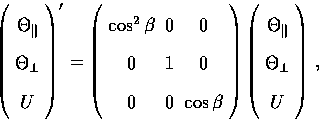
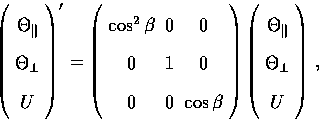
![[*]](foot_motif.gif)
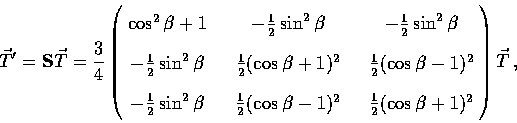
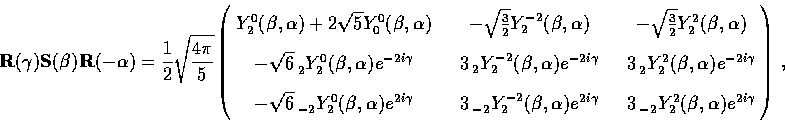
![]() in the temperature of the scattered radiation.
With the help of the generalized addition relation for the harmonics
Eqn. (7), the full collision term can be written
as
in the temperature of the scattered radiation.
With the help of the generalized addition relation for the harmonics
Eqn. (7), the full collision term can be written
as
![\begin{displaymath}
\vec{C}[{\vec {T}}] = -\dot\tau {\vec I}(\Omega) +
{1 \ove...
...sum_{m=-2}^2 {\bf P}^{(m)}(\Omega,\Omega') \vec{T}(\Omega')\, .\end{displaymath}](img201.gif)