



Next: Metric Fluctuations
Up: Scaling Stress Seeds
Previous: Scaling Stress Seeds
Stress perturbations are fundamental to seeded models
of structure formation because causality combined
with energy-momentum conservation forbids
perturbations in the energy or momentum density until matter
has had the opportunity to move around inside the horizon (see
e.g. [30]).
Isotropic stress, or pressure, only arises for scalar perturbations
and have been considered in detail by [27]. Anisotropic
stress perturbations can also come in vector and tensor types
and it is their effect that we wish to study here. Combined
they cover the full range of possibilities available to
causally seeded models such as defects.
We impose two constraints on the anisotropic stress seeds: causality
and scaling. Causality implies that correlations in the stresses
must vanish outside the horizon.
Anisotropic stresses represent spatial derivatives of
the momentum density
and hence vanish as k2 for 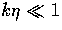 .Scaling requires that the
fundamental scale is set by the current horizon so that evolutionary
effects are a function of
.Scaling requires that the
fundamental scale is set by the current horizon so that evolutionary
effects are a function of 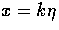 . A convenient form
that satisfies these criteria is [27,31]
. A convenient form
that satisfies these criteria is [27,31]
| 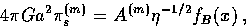 |
(78) |
with
| ![\begin{displaymath}
f_B^{}(x) = {6 \over B_2^{2} - B_1^{2}}
\left[ {\sin(B_1 x) \over (B_1 x)}
-{\sin(B_2 x) \over (B_2 x)} \right] \, ,\end{displaymath}](img377.gif) |
(79) |
with 0 < (B1,B2) < 1. We caution the reader that though
convenient and complete, this choice of basis is not
optimal for representing the currently popular set of
defect models.
It suffices for our purposes here since we only wish to
illustrate general properties of the anisotropy formation process.
Assuming B1 > B2, B1 controls the characteristic
time after horizon crossing that the stresses
are generated, i.e. the peak in fB
scales as 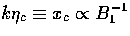 (see Fig. 7).
B2 controls the rate of decline
of the source at late times.
In the general case, the seed may be a sum of different pairs
of (B1,B2) which may also differ between scalar, vector,
and tensor components.
(see Fig. 7).
B2 controls the rate of decline
of the source at late times.
In the general case, the seed may be a sum of different pairs
of (B1,B2) which may also differ between scalar, vector,
and tensor components.
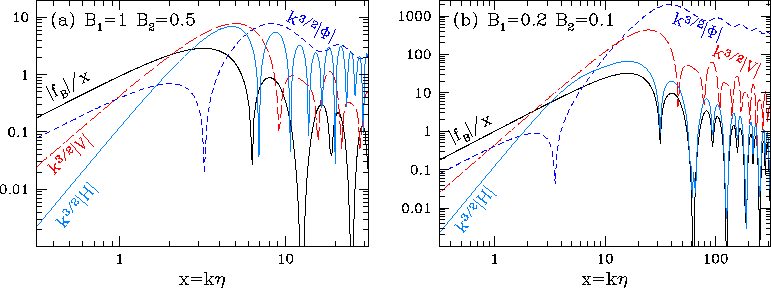
Figure 7:
Metric fluctuations from scaling anisotropic stress seeds
sources. The same anisotropic stress seed (bold solid lines
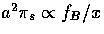 ) produce
qualitatively different scalar (short-dashed), vector (long-dashed),
and tensor (solid) metric perturbations. As discussed in the
text the behavior scales with the characteristic time of
the source
) produce
qualitatively different scalar (short-dashed), vector (long-dashed),
and tensor (solid) metric perturbations. As discussed in the
text the behavior scales with the characteristic time of
the source 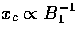 . The left panel (a) shows a source
which begins to decay as soon as causally permitted (B1=1)
and the right panel (b) the effect of delaying the decay
(B1=0.2). We have displayed the results here for a
photon-dominated universe for simplicity.
. The left panel (a) shows a source
which begins to decay as soon as causally permitted (B1=1)
and the right panel (b) the effect of delaying the decay
(B1=0.2). We have displayed the results here for a
photon-dominated universe for simplicity.
 |
Postscript:
(a)
(b)




Next: Metric Fluctuations
Up: Scaling Stress Seeds
Previous: Scaling Stress Seeds
Wayne Hu
9/9/1997
![]() .Scaling requires that the
fundamental scale is set by the current horizon so that evolutionary
effects are a function of
.Scaling requires that the
fundamental scale is set by the current horizon so that evolutionary
effects are a function of ![]() . A convenient form
that satisfies these criteria is [27,31]
. A convenient form
that satisfies these criteria is [27,31]
![\begin{displaymath}
f_B^{}(x) = {6 \over B_2^{2} - B_1^{2}}
\left[ {\sin(B_1 x) \over (B_1 x)}
-{\sin(B_2 x) \over (B_2 x)} \right] \, ,\end{displaymath}](img377.gif)
![]() (see Fig. 7).
B2 controls the rate of decline
of the source at late times.
In the general case, the seed may be a sum of different pairs
of (B1,B2) which may also differ between scalar, vector,
and tensor components.
(see Fig. 7).
B2 controls the rate of decline
of the source at late times.
In the general case, the seed may be a sum of different pairs
of (B1,B2) which may also differ between scalar, vector,
and tensor components.
