



Next: CMB Anisotropies
Up: Scaling Stress Seeds
Previous: Causal Anisotropic Stress
Let us consider how the anisotropic stress seed sources generate
scalar, vector and tensor metric fluctuations. The form
of Eqn. (101) implies that the metric perturbations
also scale so that 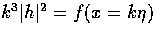 where f may be
different functions for
where f may be
different functions for 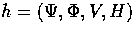 .Thus scaling in the defect field also implies scaling for
the metric evolution and consequently the purely
gravitational effects
in the CMB as we shall see in the next section. Scattering
introduces another fundamental scale, the horizon at last
scattering
.Thus scaling in the defect field also implies scaling for
the metric evolution and consequently the purely
gravitational effects
in the CMB as we shall see in the next section. Scattering
introduces another fundamental scale, the horizon at last
scattering 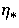 , which we shall see breaks the scaling in
the CMB.
, which we shall see breaks the scaling in
the CMB.
It is interesting to consider differences in the evolutions
for the same anisotropic stress seed, A(m)=1 with
B1 and B2 set equal for the scalars, vectors and tensors.
The basic tendencies
can be seen by considering the behavior at early times
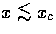 . If
. If 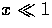 as well,
then the contributions
to the metric fluctuations scale as
as well,
then the contributions
to the metric fluctuations scale as
where fB = x2 for 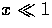 . Note that the sources
of the scalar fluctuations in this limit are the anisotropic
stress and momentum density rather than energy density
(see Eqn. 64).
This behavior is displayed
in Fig. 7(a). For the scalar and tensor evolution,
the horizon scale enters in separately from the characteristic
time xc. For the scalars, the stresses move matter around
and generate density fluctuations as
. Note that the sources
of the scalar fluctuations in this limit are the anisotropic
stress and momentum density rather than energy density
(see Eqn. 64).
This behavior is displayed
in Fig. 7(a). For the scalar and tensor evolution,
the horizon scale enters in separately from the characteristic
time xc. For the scalars, the stresses move matter around
and generate density fluctuations as 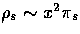 .The result is that the evolution of
.The result is that the evolution of  and
and 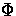 steepens by
x2 between
steepens by
x2 between 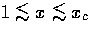 .
For the tensors, the
equation of motion takes the form of a damped driven oscillator
and whose amplitude follows the source. Thus the tensor
scaling becomes shallower in this regime. For
.
For the tensors, the
equation of motion takes the form of a damped driven oscillator
and whose amplitude follows the source. Thus the tensor
scaling becomes shallower in this regime. For 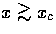 both the source and the metric fluctuations decay. Thus
the maximum metric fluctuation scales as
For a late characteristic time xc > 1, fluctuations in the
scalars are larger than vectors or tensors for the same
source (see Fig. 7b). The ratio of acoustic to
gravitational
redshift contributions from the scalars scale
as xc-2 by virtue of pressure support in
Eqn. (84)
and thus acoustic oscillations
become subdominant as B1 decreases.
both the source and the metric fluctuations decay. Thus
the maximum metric fluctuation scales as
For a late characteristic time xc > 1, fluctuations in the
scalars are larger than vectors or tensors for the same
source (see Fig. 7b). The ratio of acoustic to
gravitational
redshift contributions from the scalars scale
as xc-2 by virtue of pressure support in
Eqn. (84)
and thus acoustic oscillations
become subdominant as B1 decreases.




Next: CMB Anisotropies
Up: Scaling Stress Seeds
Previous: Causal Anisotropic Stress
Wayne Hu
9/9/1997
![]() . If
. If ![]() as well,
then the contributions
to the metric fluctuations scale as
as well,
then the contributions
to the metric fluctuations scale as

