



Next: Radial Modes
Up: Normal Modes
Previous: Normal Modes
In this section, we derive the basic properties of the angular
modes of the
temperature and polarization
distributions that will be useful in §III
to describe their evolution. In particular,
the Clebsch-Gordan relation for the addition of angular
momentum plays a central role in exposing the
simplicity of the total angular momentum representation.
A scalar, or spin- field on the sky such as the temperature
can be decomposed into spherical harmonics
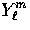 . Likewise a spin-s field on the sky
can be decomposed into the spin-weighted spherical
harmonics
. Likewise a spin-s field on the sky
can be decomposed into the spin-weighted spherical
harmonics 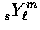 and a tensor
constructed out of the basis vectors
and a tensor
constructed out of the basis vectors
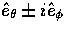 ,
,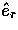 [12]. The basis
for a spin-2 field such as the polarization is
[12]. The basis
for a spin-2 field such as the polarization is
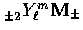 [3,4]
where
[3,4]
where
| 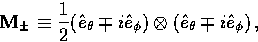 |
(1) |
since it transforms under rotations as a 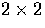 symmetric
traceless tensor. This property is more easily seen through
the relation to the
Pauli matrices,
symmetric
traceless tensor. This property is more easily seen through
the relation to the
Pauli matrices, 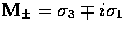 , in spherical coordinates
, in spherical coordinates 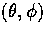 .The spin-s harmonics are expressed in terms of rotation
matrices
.The spin-s harmonics are expressed in terms of rotation
matrices![[*]](foot_motif.gif) as
[12]
The rotation matrix
as
[12]
The rotation matrix 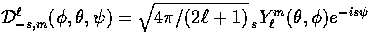 represents rotations by the Euler angles
represents rotations by the Euler angles 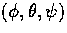 .Since the spin-2 harmonics will be useful in the following
sections, we give their explicit form in Table 1 for
.Since the spin-2 harmonics will be useful in the following
sections, we give their explicit form in Table 1 for 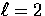 ;
the higher
;
the higher 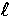 harmonics are related to the
ordinary spherical harmonics as
harmonics are related to the
ordinary spherical harmonics as
| ![\begin{displaymath}
\, {}_{\pm 2}^{\vphantom{m}} Y_{\ell}^{m} = \left[ {(\ell-2)...
...\phi - {1 \over \sin^2\theta} \partial^2_\phi \right]
Y_\ell^m.\end{displaymath}](img22.gif) |
(2) |
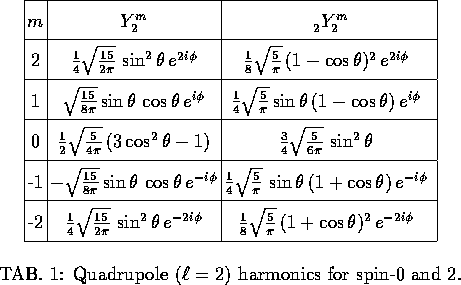
By virtue of their relation to the rotation
matrices,
the spin harmonics
satisfy: the compatibility relation
with spherical harmonics,
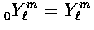 ;the conjugation relation
;the conjugation relation 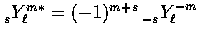 ;
the orthonormality relation,
;
the orthonormality relation,
| 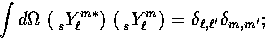 |
(3) |
the completeness relation,
| ![\begin{displaymath}
\sum_{\ell,m} \left[ \, {}_{s}^{\vphantom{m*}} Y_{\ell}^{m*}...
...right] =
\delta(\phi-\phi')\delta(\cos\theta-\cos\theta') \, ;\end{displaymath}](img27.gif) |
(4) |
the parity relation,
| 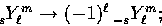 |
(5) |
the generalized addition relation,
| ![\begin{displaymath}
\sum_m \left[ \, {}_{s_1}^{\vphantom{m*}} Y_{\ell}^{m*} (\th...
... Y_{\ell}^{-s_1}
(\beta,\alpha) \right] e^{-i s_2 \gamma} \, ,\end{displaymath}](img29.gif) |
(6) |
which follows from the group multiplication property of
rotation matrices which relates a rotation from  through the origin to
through the origin to  with a direct rotation
in terms of the Euler angles
with a direct rotation
in terms of the Euler angles 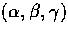 defined in Fig. 1;
and the Clebsch-Gordan relation,
defined in Fig. 1;
and the Clebsch-Gordan relation,
| 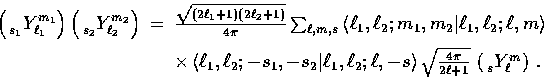 |
|
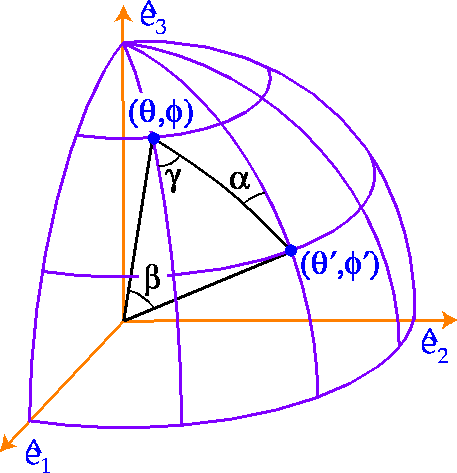
Figure 1:
Addition theorem and scattering geometry. The addition
theorem for spin-s harmonics Eqn. (7) is
established by their relation to rotations Eqn. (2)
and by noting that
a rotation from 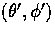 through
the origin (pole) to
through
the origin (pole) to 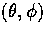 is equivalent to a direct
rotation by the Euler angles
is equivalent to a direct
rotation by the Euler angles 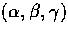 . For the
scattering problem of Eqn. (48), these angles
represent the rotation by
. For the
scattering problem of Eqn. (48), these angles
represent the rotation by 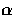 from the
from the 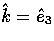 frame to the scattering frame, by the scattering angle
frame to the scattering frame, by the scattering angle 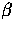 , and
by
, and
by 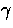 back into the
back into the 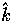 frame.
frame.
 |
It is worthwhile to examine the implications of these properties.
Note that the orthogonality and completeness relations
Eqns. (4) and (5) do not
extend to different spin states. Orthogonality between 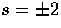 states is established by the Pauli basis of
Eqn. (1)
states is established by the Pauli basis of
Eqn. (1) 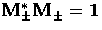 and
and 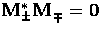 .
The parity equation (6) tells us that the
spin flips under a parity transformation so that unlike
the s=0 spherical harmonics, the higher spin harmonics are not
parity eigenstates. Orthonormal parity states can be constructed
as [3,4]
.
The parity equation (6) tells us that the
spin flips under a parity transformation so that unlike
the s=0 spherical harmonics, the higher spin harmonics are not
parity eigenstates. Orthonormal parity states can be constructed
as [3,4]
| ![\begin{displaymath}
{1 \over 2}[\, {}_{2}^{\vphantom{m}} Y_{\ell}^{m}{\bf M}_+ \pm \, {}_{-2}^{\vphantom{m}} Y_{\ell}^{m}{\bf M}_-]
\, ,\end{displaymath}](img42.gif) |
(7) |
which have ``electric'' 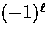 and ``magnetic''
and ``magnetic''
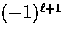 type parity for the
type parity for the
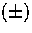 states respectively.
We shall see in §IIIC that the polarization
evolution naturally
separates into parity eigenstates. The addition property will
be useful in relating the scattering angle to coordinates
on the sphere in §IIIB. Finally
the Clebsch-Gordan relation Eqn. (8) is
central to the following discussion and will be used to derive
the total angular momentum representation in
§IIB and evolution
equations for angular moments of the radiation §IIIC.
states respectively.
We shall see in §IIIC that the polarization
evolution naturally
separates into parity eigenstates. The addition property will
be useful in relating the scattering angle to coordinates
on the sphere in §IIIB. Finally
the Clebsch-Gordan relation Eqn. (8) is
central to the following discussion and will be used to derive
the total angular momentum representation in
§IIB and evolution
equations for angular moments of the radiation §IIIC.




Next: Radial Modes
Up: Normal Modes
Previous: Normal Modes
Wayne Hu
9/9/1997
![]() . Likewise a spin-s field on the sky
can be decomposed into the spin-weighted spherical
harmonics
. Likewise a spin-s field on the sky
can be decomposed into the spin-weighted spherical
harmonics ![]() and a tensor
constructed out of the basis vectors
and a tensor
constructed out of the basis vectors
![]() ,
,![]() [12]. The basis
for a spin-2 field such as the polarization is
[12]. The basis
for a spin-2 field such as the polarization is
![]() [3,4]
where
[3,4]
where
![[*]](foot_motif.gif) as
[12]
as
[12]
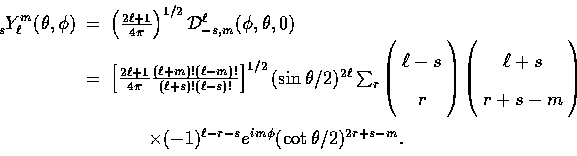
![\begin{displaymath}
\, {}_{\pm 2}^{\vphantom{m}} Y_{\ell}^{m} = \left[ {(\ell-2)...
...\phi - {1 \over \sin^2\theta} \partial^2_\phi \right]
Y_\ell^m.\end{displaymath}](img22.gif)
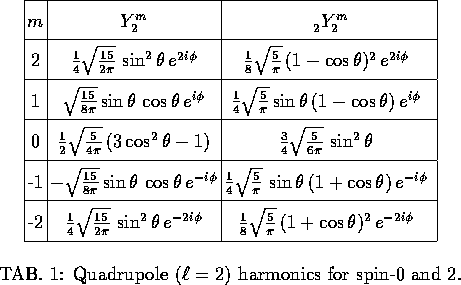
![]() ;the conjugation relation
;the conjugation relation ![]() ;
the orthonormality relation,
;
the orthonormality relation,
![\begin{displaymath}
\sum_m \left[ \, {}_{s_1}^{\vphantom{m*}} Y_{\ell}^{m*} (\th...
... Y_{\ell}^{-s_1}
(\beta,\alpha) \right] e^{-i s_2 \gamma} \, ,\end{displaymath}](img29.gif)
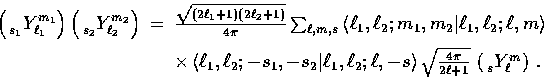

![]() states is established by the Pauli basis of
Eqn. (1)
states is established by the Pauli basis of
Eqn. (1) ![]() and
and ![]() .
The parity equation (6) tells us that the
spin flips under a parity transformation so that unlike
the s=0 spherical harmonics, the higher spin harmonics are not
parity eigenstates. Orthonormal parity states can be constructed
as [3,4]
.
The parity equation (6) tells us that the
spin flips under a parity transformation so that unlike
the s=0 spherical harmonics, the higher spin harmonics are not
parity eigenstates. Orthonormal parity states can be constructed
as [3,4]