Results

  We now employ the formalism developed here to calculate the scalar and tensor temperature and polarization power spectra for two CDM models one with critical density and one with $\Omega_0=1-\Omega_K=0.4$ with initial conditions given by Eq. (44). In general, there are two classes of effects: the geometrical and dynamical aspects of curvature.

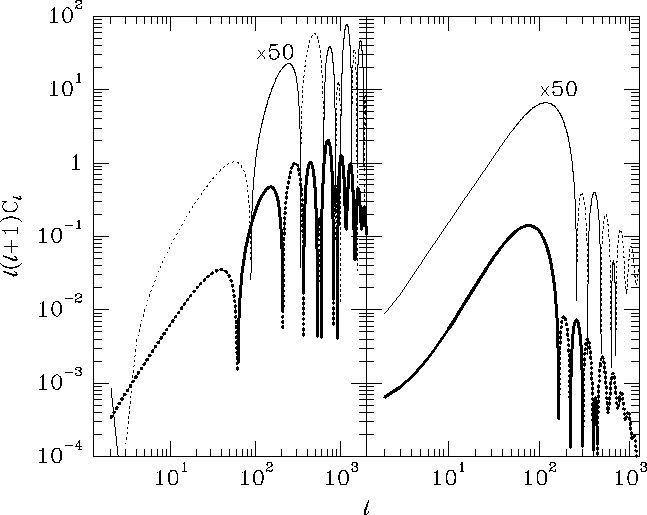
On intermediate to small scales (large $\ell$), only geometrical aspects of curvature affect the spectra. Changes in the angular diameter distance to last scattering move features in the low-$\Omega_0$ models to smaller angular scales (higher $\ell$) as discussed in §III. Since the low-$\ell$ tail of the E-mode polarization is growing rapidly with $\ell$, shifting the features to higher $\ell$ results in smaller large-angle polarization in an open model for both scalar and tensor anisotropies. The suppression is larger in the case of scalars than tensors since the low-$\ell$ slope is steeper [1].

  

Figure 2: The scalar (left) and tensor (right) temperature-polarization cross correlation $C_\ell^{\Theta E}$ with the same parameters and notation as Fig. 1 (thick: flat; thin open). Dotted lines represent negative correlation.

The presence of curvature also affects the late-time dynamics and initial power spectra. As is well known, the scalar temperature power spectrum exhibits an enhancement of power at low multipoles due to the integrated Sachs-Wolfe (ISW) effect during curvature domination. This does not affect the polarization, assuming no reionization, as it is generated at last scattering. However it does affect the temperature-polarization cross correlation (see Fig. 2). In an open universe, the largest scales (lowest $\ell$) pick up unequal-time correlations with the ISW contributions which are of opposite sign to the ordinary Sachs-Wolfe contribution. This reverses the sign of the correlation and formally violates the predictions of [20]. In practice this effect is unobservable due to the smallness of signal. Even minimal amounts of reionization will destroy this effect.

Open universe modifications to the initial power spectrum are potentially observable in the large angle CMB spectrum. Unfortunately subtle differences in the temperature power spectrum can be lost in cosmic variance. While polarization provides extra information, in the absence of late reionization the large-angle polarization is largely a projection of small scale fluctuations. Nonetheless in our universe (where reionization occured before redshift $z\approx 5$) the large-angle polarization is sensitive to the primoridial power spectrum at the curvature scale. Thus if the fluctuations which gave rise to the large-scale structure and CMB anisotropy in our universe were generated by an open inflationary scenario based on bubble nucleation, a study of the large-angle polarization can in principle teach us about the initial nucleation event [19].

In summary, we have completed the formalism for calculating and interpreting temperature and polarization anisotropies in linear theory from arbitary metric fluctuations in an FRW universe. The results presented here are new for non-flat vector and tensor (polarization) perturbations and we have calculated the scalar and tensor temperature and polarization contributions for open inflationary spectra. The open tensor perturbation equations have been added to CMBFAST which is now publically available.

truecm

Acknowledgments: We thank the Aspen Center for Physics where a portion of this work was completed. W.H was supported by the W.M. Keck Foundation and M.Z. by NASA Grant NAG5-2816.