



Next: Metric and Scattering Sources
Up: A COMPLETE TREATMENT OF
Previous: Perturbation Representation
The Boltzmann equation describes the evolution in time 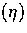 of the
spatial (
of the
spatial (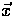 ) and angular (
) and angular (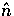 ) distribution of the radiation
under gravity and scattering processes. In the notation of [1], it
can be written implicitly as
) distribution of the radiation
under gravity and scattering processes. In the notation of [1], it
can be written implicitly as
| ![\begin{displaymath}
{d \over d\eta} \vec{T}(\eta,\vec{x},\hat{n}) \equiv
{\part...
...vec{T}_{\vert i}
= \vec{C}[\vec{T}] + \vec{G}[h_{\mu\nu}] \, ,\end{displaymath}](img52.gif) |
(14) |
where 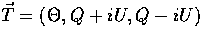 encapsulates the perturbation
to the temperature
encapsulates the perturbation
to the temperature 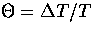 and the polarization
(Stokes Q and U parameters) in units of the temperature fluctuation.
The term
and the polarization
(Stokes Q and U parameters) in units of the temperature fluctuation.
The term 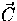 accounts for collisions, here Compton scattering of the
photons with the electrons,
while the term
accounts for collisions, here Compton scattering of the
photons with the electrons,
while the term 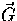 accounts for gravitational redshifts.
accounts for gravitational redshifts.
Wayne Hu
9/9/1997