Polarization provides a more direct test in that it can only be generated through scattering. The large angle polarization reflects fluctuations near the horizon at last scattering and so may provide a direct window on such causal, non-inflationary models of structure formation. One must be careful however to separate scalar, vector and tensor modes whose different large angle behaviors may obscure the issue. Let us now illustrate these considerations with the specific examples introduced in the last section.
The metric fluctuations produced by the seed sources
generate CMB anisotropies through the Boltzmann
equation
(60).
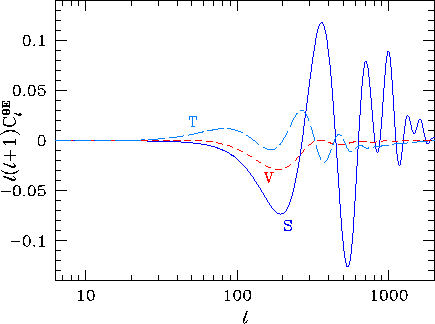
We display an example with B1=1 and
B2=0.5 in Fig. 8. Notice that
scaling in the sources does indeed lead to near scale invariance
in the large angle temperature but not the large angle polarization.
The small rise toward the quadrupole for the tensor temperature
is due to
the contribution of long-wavelength gravity waves that are
currently being generated and depends on how rapidly they
are generated after horizon crossing.
Inside the horizon at last scattering (here ![]() ),
scalar fluctuations generate acoustic waves as discussed in
§IV which dominate for small characteristic
times
),
scalar fluctuations generate acoustic waves as discussed in
§IV which dominate for small characteristic
times ![]() .
On the other hand, these contributions are strongly
damped below the thickness of the last scattering surface
by dissipational processes. Note that features in the vector
and tensor spectrum shown here are artifacts of our choice of
source function. In a realistic model, the superposition of
many sources of this type will wash out such features. The
general tendencies however do not depend on the detailed form
of the source. Note that vector and tensor contributions
damp more slowly and hence may contribute significantly
to the small-angle temperature anisotropy.
.
On the other hand, these contributions are strongly
damped below the thickness of the last scattering surface
by dissipational processes. Note that features in the vector
and tensor spectrum shown here are artifacts of our choice of
source function. In a realistic model, the superposition of
many sources of this type will wash out such features. The
general tendencies however do not depend on the detailed form
of the source. Note that vector and tensor contributions
damp more slowly and hence may contribute significantly
to the small-angle temperature anisotropy.
Polarization can only be generated by scattering of a quadrupole
temperature anisotropy.
For seeded models, scales outside the horizon
at last scattering ![]() have not formed significant metric fluctuations
(see e.g. Fig. 7). Hence quadrupole fluctuations,
generated from the metric fluctuations through
Eqns. (90),
(92), and (93), are also suppressed.
The power in k of the polarization thus drops sharply
below
have not formed significant metric fluctuations
(see e.g. Fig. 7). Hence quadrupole fluctuations,
generated from the metric fluctuations through
Eqns. (90),
(92), and (93), are also suppressed.
The power in k of the polarization thus drops sharply
below
![]() . This drop of course corresponds to a lack of
large angle power in the polarization. However its form at
low
. This drop of course corresponds to a lack of
large angle power in the polarization. However its form at
low ![]() depends on geometric aspects of the projection from
k to
depends on geometric aspects of the projection from
k to ![]() . In these models, the large
angle polarization is dominated
by projection aliasing of power from small scales
. In these models, the large
angle polarization is dominated
by projection aliasing of power from small scales ![]() . The asymptotic expressions of Eqn. (77)
thus determine the large angle behavior of the polarization:
. The asymptotic expressions of Eqn. (77)
thus determine the large angle behavior of the polarization:
![]() for scalars (EE),
for scalars (EE),
![]() for vectors
and
for vectors
and ![]() for tensors (EE and BB); the cross spectrum
for tensors (EE and BB); the cross spectrum
![]() goes as
goes as ![]() for each contribution.
For comparison, the scale invariant
adiabatic
inflationary prediction has scalar
polarization (EE) dropping off as
for each contribution.
For comparison, the scale invariant
adiabatic
inflationary prediction has scalar
polarization (EE) dropping off as ![]() and cross
spectrum (
and cross
spectrum (![]() ) as
) as ![]() from Eqn. (92) because of the constant
potential above the horizon (see Fig. 6).
Seeded models thus predict a more rapid reduction in the
scalar polarization
for the same background cosmology.
from Eqn. (92) because of the constant
potential above the horizon (see Fig. 6).
Seeded models thus predict a more rapid reduction in the
scalar polarization
for the same background cosmology.
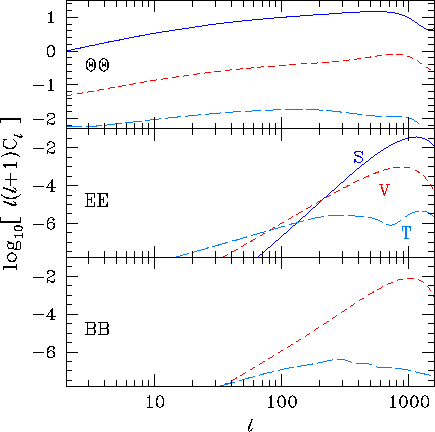
Polarization can also help separate the three types of fluctuations.
In accord with the general prediction (see §IIID),
scalars produce no B-parity polarization, whereas
vector B-parity dominates E-parity polarization
by a factor of 6 and tensor B-parity is suppressed
by a factor of 8/13 (see Eqn. (23)).
Differences also arise in the temperature-polarization
cross power spectra ![]() shown in Fig. 9.
Independent of the nature of the source, above the angle the
horizon subtends at last scattering, scalar and vector temperature
perturbations from the last scattering surface [21]
are anticorrelated with polarization, whereas they are correlated for
tensor perturbations (see §IVB
and [9]). Inside
the horizon, the scalar polarization follows the scalar
velocity which is
shown in Fig. 9.
Independent of the nature of the source, above the angle the
horizon subtends at last scattering, scalar and vector temperature
perturbations from the last scattering surface [21]
are anticorrelated with polarization, whereas they are correlated for
tensor perturbations (see §IVB
and [9]). Inside
the horizon, the scalar polarization follows the scalar
velocity which is ![]() out of phase with the effective
temperature (see Eqn. 89).
In the adiabatic model, scalar cross correlation reverses
signs before the first acoustic peak, as compression overcomes
the gravitational redshift of the Sachs-Wolfe effect, unlike the
isocurvature models (see Fig. 6 and [28]).
The sign test to
distinguish scalars from tensors must thus be performed on
scales larger than twice the first peak. Conversely, to use
the cross correlation to distinguish adiabatic from isocurvature
fluctuations, the scalar and tensor contributions must be
separated.
out of phase with the effective
temperature (see Eqn. 89).
In the adiabatic model, scalar cross correlation reverses
signs before the first acoustic peak, as compression overcomes
the gravitational redshift of the Sachs-Wolfe effect, unlike the
isocurvature models (see Fig. 6 and [28]).
The sign test to
distinguish scalars from tensors must thus be performed on
scales larger than twice the first peak. Conversely, to use
the cross correlation to distinguish adiabatic from isocurvature
fluctuations, the scalar and tensor contributions must be
separated.
|
How do these results change with the model for the seeds? As we increase the characteristic time xc by decreasing B1=0.2 (see Fig. 10), the main effect comes from differences in the generation of metric fluctuations discussed in §VB. For the same amplitude anisotropic stress, scalars contributions dominate the vector and tensor contributions by factors of xc = B1-1 (see Eqn. 103). Note however that the scalar contributions come from the gravitational redshifts between last scattering and today rather than the acoustic oscillations (see §IVA) and hence produce no strong features. Because of the late generation of metric fluctuations in these models, the peak in the polarization spectra is also shifted with xc. Note however that the qualitative behavior of the polarization described above remains the same.
 |
Although these examples do not exhaust the full range of possibilities
for scaling seeded models, the general behavior is representative.
Equal amplitude anisotropic stress sources tend to produce
similar large angle temperature anisotropies if the source is
active as soon as causally allowed ![]() . Large
angle scalar polarization is reduced as compared with
adiabatic inflationary models because of causal constraints
on their formation.
This behavior is not as marked in vectors and tensors
due to the projection geometry
but the relative amplitudes of the E-parity and B-parity
polarization as well as the
. Large
angle scalar polarization is reduced as compared with
adiabatic inflationary models because of causal constraints
on their formation.
This behavior is not as marked in vectors and tensors
due to the projection geometry
but the relative amplitudes of the E-parity and B-parity
polarization as well as the ![]() cross correlation
can be used to separate them independently
of assumptions for the seed sources. Of course in practice
these tests at large angles will be difficult to apply due
to the smallness of the expected signal.
cross correlation
can be used to separate them independently
of assumptions for the seed sources. Of course in practice
these tests at large angles will be difficult to apply due
to the smallness of the expected signal.
Reionization increases the large angle polarization signal because the quadrupole anisotropies that generate it can be much larger [32]. This occurs since decoupling occurs gradually and the scattering is no longer rapid enough to suppress anisotropies. The prospects for separating the scalars, vectors and tensors based on polarization consequently also improve [33].
For angles smaller than that subtended by the horizon at last scattering, the relative contributions of these effects depends on a competition between scalar gravitational and acoustic effects and the differences in the generation and damping behavior of the scalar, vector and tensor perturbations.