



Next: Viscosity and Polarization
Up: Photon-Baryon Fluid
Previous: Photon-Baryon Fluid
For the (m=0) scalars, the well-known result of expanding
the Boltzmann equations (60) for 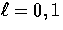 and the baryon
Euler equation (67) is
which represent the photon fluid continuity and Euler equations
and gives the baryon fluid quantities directly as
and the baryon
Euler equation (67) is
which represent the photon fluid continuity and Euler equations
and gives the baryon fluid quantities directly as
| 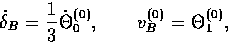 |
(64) |
to lowest order. Here 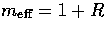 where recall that R is
the baryon-photon momentum density ratio.
We have dropped the viscosity term
where recall that R is
the baryon-photon momentum density ratio.
We have dropped the viscosity term
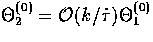 (see §
IVB).
The effect of the baryons is to introduce a Compton drag term that
slows the oscillation and
enhances infall into gravitational potential wells
(see §
IVB).
The effect of the baryons is to introduce a Compton drag term that
slows the oscillation and
enhances infall into gravitational potential wells 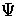 . That these
equations describe forced acoustic oscillations in the fluid is
clear when we rewrite the equations as
. That these
equations describe forced acoustic oscillations in the fluid is
clear when we rewrite the equations as
| 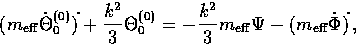 |
(65) |
whose solution in the absence of metric fluctuations
is
where 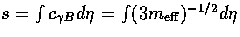 is the sound horizon, A is
a constant amplitude and
is the sound horizon, A is
a constant amplitude and 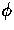 is
a constant phase shift.
In the presence of potential perturbations,
the redshift a photon experiences
climbing out of a potential well makes the effective temperature
is
a constant phase shift.
In the presence of potential perturbations,
the redshift a photon experiences
climbing out of a potential well makes the effective temperature
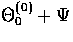 (see Eqn. 78),
which satisfies
(see Eqn. 78),
which satisfies
| ![\begin{displaymath}[m_{\rm eff} (\dot\Theta_0^{(0)}+\dot\Psi)]
\,\dot{\vphantom{...
...si +
[m_{\rm eff}(\dot\Psi - \dot\Phi)]\,\dot{\vphantom{A}} ,\end{displaymath}](img317.gif) |
(66) |
and shows that the effective force on the oscillator is due
to baryon drag 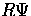 and differential gravitational redshifts
from the time dependence of the metric.
As seen in Eqn. (78)
and (83),
the effective temperature
at last scattering forms the main contribution at last scattering
with the Doppler effect
and differential gravitational redshifts
from the time dependence of the metric.
As seen in Eqn. (78)
and (83),
the effective temperature
at last scattering forms the main contribution at last scattering
with the Doppler effect 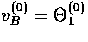 playing a secondary role for
playing a secondary role for 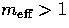 . Furthermore,
because of the nature
of the monopole versus dipole projection, features in
. Furthermore,
because of the nature
of the monopole versus dipole projection, features in 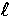 space are mainly created by the effective temperature
(see Fig. 3 and §IIID).
space are mainly created by the effective temperature
(see Fig. 3 and §IIID).
If
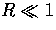 , then one expects contributions of
, then one expects contributions of
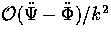 to the oscillations
in
to the oscillations
in 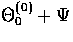 in addition to the initial fluctuations.
These acoustic contributions should be compared with the
in addition to the initial fluctuations.
These acoustic contributions should be compared with the
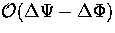 contributions from gravitational
redshifts in a time dependent metric after last scattering.
The stimulation of oscillations at
contributions from gravitational
redshifts in a time dependent metric after last scattering.
The stimulation of oscillations at 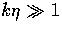 thus either
requires large or rapidly varying metric fluctuations. In
the case of the former, acoustic oscillations would be small
compared to gravitational redshift contributions.
thus either
requires large or rapidly varying metric fluctuations. In
the case of the former, acoustic oscillations would be small
compared to gravitational redshift contributions.
Vector perturbations on the other hand lack pressure support
and cannot generate acoustic
or compressional waves. The
tight coupling expansion of the photon 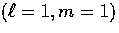 and baryon Euler
equations (60) and (71)
leads to
and baryon Euler
equations (60) and (71)
leads to
| ![\begin{displaymath}[ m_{\rm eff} (\Theta^{(1)}_1 - V) ]
\dot{\hphantom{A}} = 0 \, ,\end{displaymath}](img326.gif) |
(67) |
and 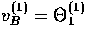 . Thus the vorticity in the
photon baryon fluid is of equal amplitude to the vector
metric perturbation. In the absence of sources, it is
constant in a photon-dominated fluid and decays as
a-1 with the expansion in a baryon-dominated fluid.
In the presence of sources, the solution
is
. Thus the vorticity in the
photon baryon fluid is of equal amplitude to the vector
metric perturbation. In the absence of sources, it is
constant in a photon-dominated fluid and decays as
a-1 with the expansion in a baryon-dominated fluid.
In the presence of sources, the solution
is
| ![\begin{displaymath}
\Theta^{(1)}_1(\eta,k) = V(\eta,k) + {1 \over m_{\rm eff}}
[\Theta^{(1)}(0,k)-V(0,k)] \, ,\end{displaymath}](img328.gif) |
(68) |
so that the photon dipole tracks the evolution of the metric
fluctuation. With 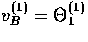 in
Eqn. (61), vorticity
leads to a Doppler effect in the CMB of magnitude
on order the vector metric fluctuation at last scattering V in
contrast to scalar acoustic effects which depend on the time
rate of change of the metric.
in
Eqn. (61), vorticity
leads to a Doppler effect in the CMB of magnitude
on order the vector metric fluctuation at last scattering V in
contrast to scalar acoustic effects which depend on the time
rate of change of the metric.
In turn the vector metric
depends on the vector anisotropic stress of the matter
as
| 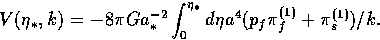 |
(69) |
In the absence of sources 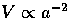 and decays with
the expansion. They are thus generally negligible if the universe
contains only the usual fluids. Only seeded models such as cosmological
defects may have their contributions to
the CMB anisotropy dominated by vector modes.
However even though the vector to scalar fluid
contribution to the anisotropy for seeded models is of order
and decays with
the expansion. They are thus generally negligible if the universe
contains only the usual fluids. Only seeded models such as cosmological
defects may have their contributions to
the CMB anisotropy dominated by vector modes.
However even though the vector to scalar fluid
contribution to the anisotropy for seeded models is of order
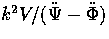 and may be large,
the vector to scalar
gravitational redshift contributions, of order
and may be large,
the vector to scalar
gravitational redshift contributions, of order
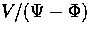 is not necessarily large. Furthermore from
the integral solution for the vectors
Eqn. (78) and the tight coupling
approximation Eqn. (86), the fluid effects
tend to cancel part of the gravitational effect.
is not necessarily large. Furthermore from
the integral solution for the vectors
Eqn. (78) and the tight coupling
approximation Eqn. (86), the fluid effects
tend to cancel part of the gravitational effect.




Next: Viscosity and Polarization
Up: Photon-Baryon Fluid
Previous: Photon-Baryon Fluid
Wayne Hu
9/9/1997
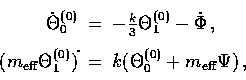
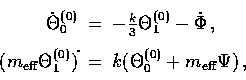
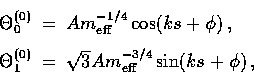
![]() , then one expects contributions of
, then one expects contributions of
![]() to the oscillations
in
to the oscillations
in ![]() in addition to the initial fluctuations.
These acoustic contributions should be compared with the
in addition to the initial fluctuations.
These acoustic contributions should be compared with the
![]() contributions from gravitational
redshifts in a time dependent metric after last scattering.
The stimulation of oscillations at
contributions from gravitational
redshifts in a time dependent metric after last scattering.
The stimulation of oscillations at ![]() thus either
requires large or rapidly varying metric fluctuations. In
the case of the former, acoustic oscillations would be small
compared to gravitational redshift contributions.
thus either
requires large or rapidly varying metric fluctuations. In
the case of the former, acoustic oscillations would be small
compared to gravitational redshift contributions.
![]() and baryon Euler
equations (60) and (71)
leads to
and baryon Euler
equations (60) and (71)
leads to