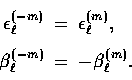Next: Interpretation
Up: Radial Modes
Previous: Radial Modes
The temperature and polarization distribution of the radiation
is in general a function of both spatial position  and angle
and angle
 defining the propagation direction.
In flat space, we know that
plane waves form a complete basis for the spatial dependence.
Thus a spin- field like the temperature may be expanded in
defining the propagation direction.
In flat space, we know that
plane waves form a complete basis for the spatial dependence.
Thus a spin- field like the temperature may be expanded in
| 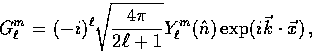 |
(8) |
where the normalization is chosen to agree with the standard
Legendre polynomial conventions for m=0.
Likewise a spin-2 field like the polarization may be expanded in
| ![\begin{displaymath}
{}_{\pm 2}G_\ell^m =
(-i)^\ell \sqrt{ {4\pi \over 2\ell+1}}...
...tom{m}} Y_{\ell}^{m}(\hat{n})] \exp(i\vec{k} \cdot \vec{x})\, .\end{displaymath}](img49.gif) |
(9) |
The plane wave itself also carries an angular dependence of course,
| 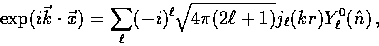 |
(10) |
where 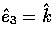 and
and
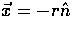 (see Fig. 2).
The sign convention for the direction is opposite
to direction on the sky to be in accord with the direction of
propagation of the radiation to the observer. Thus the extra factor
of
(see Fig. 2).
The sign convention for the direction is opposite
to direction on the sky to be in accord with the direction of
propagation of the radiation to the observer. Thus the extra factor
of 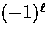 comes from the parity relation Eqn. (6).
comes from the parity relation Eqn. (6).
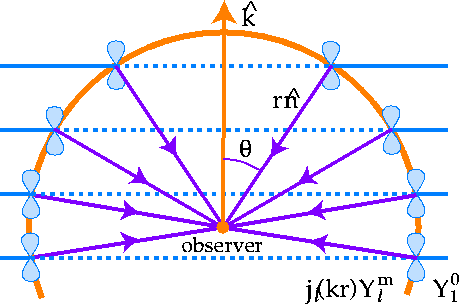
Figure 2:
Projection effects. A plane wave 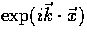 can be decomposed into
can be decomposed into 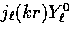 and
hence carries an ``orbital'' angular dependence. A
plane wave source at distance r thus contributes
angular power to
and
hence carries an ``orbital'' angular dependence. A
plane wave source at distance r thus contributes
angular power to 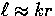 at
at 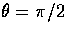 but also
to larger angles
but also
to larger angles 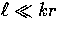 at
at 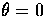 which is
encapsulated into the structure of
which is
encapsulated into the structure of 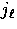 (see Fig. 3). If the source has an intrinsic
angular dependence, the distribution of power is altered. For
an aligned dipole
(see Fig. 3). If the source has an intrinsic
angular dependence, the distribution of power is altered. For
an aligned dipole 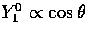 (`figure 8's) power at
(`figure 8's) power at 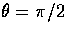 or
or
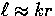 is suppressed. These arguments are generalized
for other intrinsic angular dependences in the text.
is suppressed. These arguments are generalized
for other intrinsic angular dependences in the text.
 |
The separation of the mode functions into an intrinsic angular
dependence and plane-wave spatial dependence is essentially
a division into spin (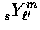 ) and orbital
(
) and orbital
(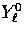 ) angular momentum. Since only
the total angular dependence is observable, it is instructive
to employ the Clebsch-Gordan relation of
Eqn. (8) to add the angular momenta.
In general this couples the states between
) angular momentum. Since only
the total angular dependence is observable, it is instructive
to employ the Clebsch-Gordan relation of
Eqn. (8) to add the angular momenta.
In general this couples the states between
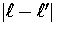 and
and 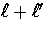 . Correspondingly
a state of definite total
. Correspondingly
a state of definite total 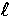 will correspond to a weighted
sum of
will correspond to a weighted
sum of 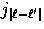 to
to 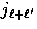 in its radial
dependence. This can be reexpressed in terms of
the
in its radial
dependence. This can be reexpressed in terms of
the 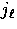 using the recursion
relations of spherical Bessel functions,
using the recursion
relations of spherical Bessel functions,
We can then rewrite
| 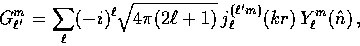 |
(11) |
where the lowest 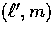 radial functions are
radial functions are
| 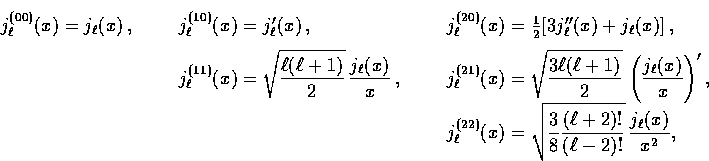 |
(12) |
with primes representing derivatives with respect to the argument
of the radial function x=kr.
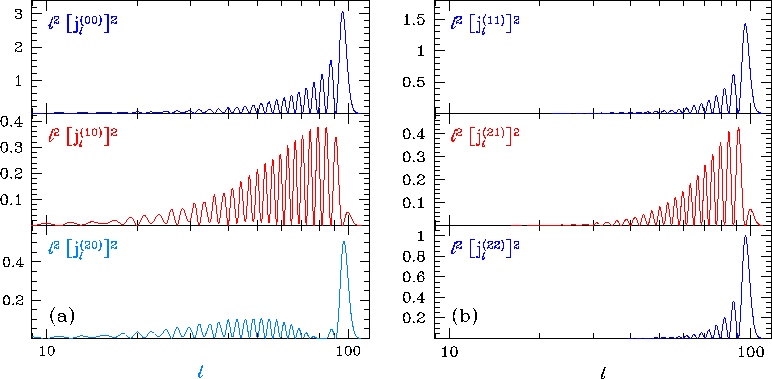
These modes are shown in Fig. 3.
Figure 3:
Radial spin-0 (temperature) modes.
The angular power in a plane wave (left panel, top)
is modified due to the intrinsic
angular structure of the source as discussed in the text.
The left panel corresponds to the power in scalar (m=0)
monopole G00, dipole G10, and quadrupole G20
sources (top to bottom);
the right panel to that in vector (m=1) dipole 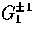 and quadrupole
and quadrupole 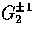 sources and a tensor (m=2)
quadrupole
sources and a tensor (m=2)
quadrupole 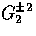 source (top to bottom).
Note the differences
in how sharply peaked the power is at
source (top to bottom).
Note the differences
in how sharply peaked the power is at 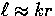 and
how fast power falls as
and
how fast power falls as 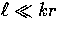 .The argument of the radial functions kr=100 here.
.The argument of the radial functions kr=100 here.
 |
Postscript:
(a)
(b)
Similarly for the spin 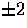 functions with m>0 (see
Fig. 4),
functions with m>0 (see
Fig. 4),
| ![\begin{displaymath}
{}_{\pm 2} G_2^m
= \sum_\ell (-i)^\ell \sqrt{4\pi(2\ell+1)...
...)] \,
\, {}_{\pm 2}^{\vphantom{m}} Y_{\ell}^{m}(\hat{n}) \, ,\end{displaymath}](img77.gif) |
(13) |
where
which corresponds to the 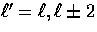 coupling and
which corresponds to the
coupling and
which corresponds to the 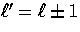 coupling.
The corresponding relation for negative m involves a reversal
in sign of the
coupling.
The corresponding relation for negative m involves a reversal
in sign of the 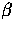 -functions
These functions are plotted in Fig. 4.
Note that
-functions
These functions are plotted in Fig. 4.
Note that 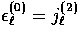 is displayed
in Fig. 3.
is displayed
in Fig. 3.
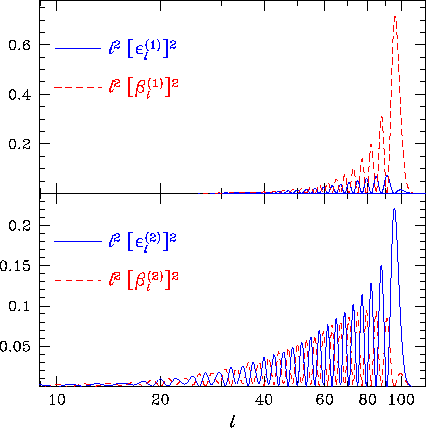
Figure 4:
Radial spin-2 (polarization) modes. Displayed is
the angular power in a plane-wave spin-2 source. The top panel
shows that vector (m=1, upper panel)
sources are dominated by B-parity
contributions, whereas tensor (m=2, lower panel) sources have
comparable but less power in the B-parity. Note that the power is strongly
peaked at 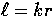 for the B-parity vectors and E-parity
tensors.
The argument of the radial functions kr=100 here.
for the B-parity vectors and E-parity
tensors.
The argument of the radial functions kr=100 here.
 |




Next: Interpretation
Up: Radial Modes
Previous: Radial Modes
Wayne Hu
9/9/1997
![]() and angle
and angle
![]() defining the propagation direction.
In flat space, we know that
plane waves form a complete basis for the spatial dependence.
Thus a spin- field like the temperature may be expanded in
defining the propagation direction.
In flat space, we know that
plane waves form a complete basis for the spatial dependence.
Thus a spin- field like the temperature may be expanded in
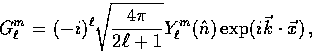
![\begin{displaymath}
{}_{\pm 2}G_\ell^m =
(-i)^\ell \sqrt{ {4\pi \over 2\ell+1}}...
...tom{m}} Y_{\ell}^{m}(\hat{n})] \exp(i\vec{k} \cdot \vec{x})\, .\end{displaymath}](img49.gif)

![]() ) and orbital
(
) and orbital
(![]() ) angular momentum. Since only
the total angular dependence is observable, it is instructive
to employ the Clebsch-Gordan relation of
Eqn. (8) to add the angular momenta.
In general this couples the states between
) angular momentum. Since only
the total angular dependence is observable, it is instructive
to employ the Clebsch-Gordan relation of
Eqn. (8) to add the angular momenta.
In general this couples the states between
![]() and
and ![]() . Correspondingly
a state of definite total
. Correspondingly
a state of definite total ![]() will correspond to a weighted
sum of
will correspond to a weighted
sum of ![]() to
to ![]() in its radial
dependence. This can be reexpressed in terms of
the
in its radial
dependence. This can be reexpressed in terms of
the ![]() using the recursion
relations of spherical Bessel functions,
using the recursion
relations of spherical Bessel functions,
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}{j_\ell(x) \over x} &=& {1...
...\ell j_{\ell-1}(x) -
(\ell +1) j_{\ell+1}(x) ] \,.\end{array}\end{displaymath}](img68.gif)
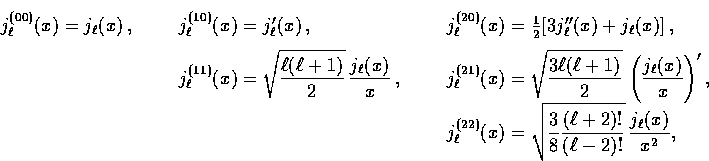

![]() functions with m>0 (see
Fig. 4),
functions with m>0 (see
Fig. 4),
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}\epsilon^{(0)}_\ell(x) & =...
...(x) \over x^2} +
4{j_\ell'(x) \over x} \right] \, ,\end{array}\end{displaymath}](img78.gif)
![\begin{displaymath}
\begin{array}
{rcl}\displaystyle{}\beta^{(0)}_\ell(x) &=& 0\...
...ft[ j_\ell'(x)
+ 2 {j_\ell(x) \over x} \right] \, ,\end{array}\end{displaymath}](img80.gif)