Interpretation

The structure of these functions is readily apparent from geometrical considerations. A single plane wave contributes to a range of angular scales from $\ell \approx kr$ at $\theta=\pi/2$ to larger angles $\ell \ll kr$as $\theta \rightarrow (0,\pi)$, where $\hat{k} \cdot \hat{n} = \cos\theta$ (see Fig. 1). The power in $\ell$ of a single plane wave shown in Fig. 3(a) (top panel) drops to zero $\ell \agt kr$, has a concentration of power around $\ell = kr$ and an extended low amplitude tail to $\ell \alt kr$.

Now if the plane wave is multiplied by an intrinsic angular dependence, the projected power changes. The key to understanding this effect is to note that the intrinsic angular behavior is related to power in $\ell$as

$$\begin{array} {rcl}\displaystyle{}\theta \rightarrow (0,\pi)... ...& \Longleftrightarrow & \qquad \ell \approx kr \, .\end{array}$$

Thus factors of $\sin\theta$ in the intrinsic angular dependence suppress power at $\ell \ll kr$ (``aliasing suppression''), whereas factors of $\cos\theta$ suppress power at $\ell \approx kr$(``projection suppression''). Let us consider first a m=0 dipole contribution $Y_1^0 \propto \cos\theta$ (see Fig. 2). The $\cos\theta$ dependence suppresses power in $j_\ell^{(10)}$ at the peak in the plane-wave spectrum $\ell \approx kr$ (compare Fig. 3(a) top and middle panels). The remaining power is broadly distributed for $\ell \alt kr$. The same reasoning applies for Y₂⁰ quadrupole sources which have an intrinsic angular dependence of $3\cos^2\theta - 1$. Now the minimum falls at $\theta = \cos^{-1}(1/\sqrt{3})$causing the double peaked form of the power in $j_\ell^{(20)}$shown in Fig. 3(a) (bottom panel). This series can be continued to higher $G_\ell^0$ and such techniques have been used in the free streaming limit for temperature anisotropies [11].

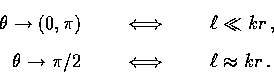Similarly, the structures of $j_\ell^{(11)}$, $j_\ell^{(21)}$and $j_\ell^{(22)}$ are apparent from the intrinsic angular dependences of the G₁¹, G₂¹ and G₂² sources,

$$Y_1^1 \propto \sin\theta e^{i\phi}\, , \qquad Y_2^1 \propto ... ...e^{i\phi} \, , \qquad Y_2^2 \propto \sin^2\theta e^{2i\phi}\, ,$$ (14)

respectively. The $\sin\theta$ factors imply that as m increases, low $\ell$ power in the source decreases (compare Fig. 3(a,b) top panels). G₂¹ suffers a further suppression at $\theta=\pi/2$ $(\ell \approx kr)$ from its $\cos\theta$ factor.

There are two interesting consequences of this behavior. The sharpness of the radial function around $\ell = kr$ quantifies how faithfully features in the k-space spectrum are preserved in $\ell$-space. If all else is equal, this faithfulness increases with |m| for G_|m|^m due to aliasing suppression from $\sin^m\theta.$ On the other hand, features in G_|m|+1^m are washed out in comparison due projection suppression from the $\cos\theta$ factor.

Secondly, even if there are no contributions from long wavelength sources with $k \ll \ell/r$, there will still be large angle anisotropies at $\ell \ll kr$ which scale as  

$$[\ell j_\ell^{(\ell'm)}] ^2 \propto \ell^{2+2\vert m\vert}.$$ (15)

This scaling puts an upper bound on how steeply the power can rise with $\ell$ that increases with |m| and hence a lower bound on the amount of large relative to small angle power that decreases with |m|.

The same arguments apply to the spin-2 functions with the added complication of the appearance of two radial functions $\epsilon_\ell$ and $\beta_\ell$. The addition of spin-2 angular momenta introduces a $\beta$-contribution from $e^{im\phi}$except for m=0. For $m = \pm 1$, the $\beta$-contribution strongly dominates over the $\epsilon$-contributions; whereas for $m = \pm 2$, $\epsilon$-contributions are slightly larger than $\beta$-contributions (see Fig. 4). The ratios reach the asymptotic values of  

$${\sum_\ell [\ell \beta_\ell^{(m)} ]^2 \over \sum_\ell [\el... ...es{ 6, & $m= \pm 1,$\space \cr 8/13, & $m= \pm 2,$\space \cr}$$ (16)

for fixed $kr \gg 1$. These considerations are closely related to the parity of the multipole expansion. Although the orbital angular momentum does not mix states of different spin, it does mix states of different parity since the plane wave itself does not have definite parity. A state with ``electric'' parity in the intrinsic angular dependence (see Eqn. 9) becomes 

$$\begin{array} {rcl}\displaystyle{}{}_{2}^{\vphantom{2}} G_... ...}_{-2}^{\vphantom{m}} Y_{\ell}^{m}{\bf M}_-] \Big\}.\end{array}$$

Thus the addition of angular momentum of the plane wave generates ``magnetic'' B-type parity of amplitude $\beta_\ell$ out of an intrinsically ``electric'' E-type source as well as E-type parity of amplitude $\epsilon_\ell$.Thus the behavior of the two radial functions has significant consequences for the polarization calculation in §IIIC and implies that B-parity polarization is absent for scalars, dominant for vectors, and comparable to but slightly smaller than the E-parity for tensors.

Now let us consider the low $\ell \ll kr$ tail of the spin-2 radial functions. Unlike the spin-0 projection, the spin-2 projection allows increasingly more power at $\theta \rightarrow 0$ and/or $\pi$,i.e. $\ell \ll kr$, as |m| increases (see Table 1 and note the factors of $\sin\theta$). In this limit, the power in a plane wave fluctuation goes as  

$$[\ell \epsilon_\ell^{(m)}] ^2 \propto \ell^{6 - 2\vert m\vert... ...ad [\ell \beta_\ell^{(m)}]^2 \propto \ell^{6 - 2\vert m\vert}.$$ (17)

Comparing these expressions with Eqn. (22), we note that the spin- and spin-2 functions have an opposite dependence on m. The consequence is that the relative power in large vs. small angle polarization tends to decrease from the m=2 tensors to the m=0 scalars.

Finally it is interesting to consider the cross power between spin- and spin-2 sources because it will be used to represent the temperature-polarization cross correlation. Again interesting geometric effects can be identified (see Fig. 5). For m=0, the power in $j_\ell^{(00)} \epsilon_\ell^{(0)}$correlates (Fig. 5, top panel solid line, positive definite); for m= 1, $j_\ell^{(11)}\epsilon_\ell^{(1)}$ oscillates (short dashed line) and for m=2, $j_\ell^{(22)} \epsilon_\ell^{(2)}$ anticorrelates (long dashed line, negative definite). The cross power involves only $\epsilon_\ell^{(m)} j_\ell^{(\ell'm)}$due to the opposite parity of the $\beta_\ell^{(m)}$ modes.

  

Figure 5: Spin-0 $\times$ Spin-2 (temperature $\times$ polarization) modes. Displayed is the cross angular power in plane wave spin-0 and spin-2 sources. The top panel shows that a scalar monopole (m=0) source correlates with a scalar spin-2 (polarization quadrupole) source whereas the tensor quadrupole (m=2) anticorrelates with a tensor spin-2 source. Vector dipole (m=1) sources oscillate in their correlation with vector spin-2 sources and contribute negligible once modes are superimposed. One must go to vector quadrupole sources (lower panel) for a strong correlation. The argument of the radial functions kr=100 here.

These properties will become important in § III and IVB and translates into cross power contributions with opposite sign between the scalar monopole temperature cross polarization sources and tensor quadrupole temperature cross polarization sources [9]. Vector dipole temperature and polarization sources do not contribute strongly to the cross power since correlations and anticorrelations in $j_\ell^{(11)}\epsilon_\ell^{(1)}$will cancel when modes are superimposed. The same is true of the scalar dipole temperature cross polarization $j_\ell^{(10)} \epsilon_\ell^{(0)}$as is apparent from Figs. 3 and 4. The vector cross power is dominated by quadrupole temperature and polarization sources $j_\ell^{(21)}\epsilon_\ell^{(1)}$(Fig. 5 lower panel).