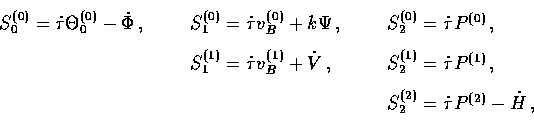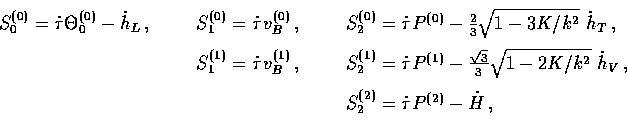Next: Integral Solutions
Up: Boltzmann Equation
Previous: Normal Modes
It is now straightforward to rewrite the Boltzmann equation
(19) as the evolution equations for the amplitudes
of the normal modes of the temperature and polarization
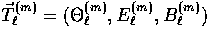 .The gravitational sources and scattering sources of these equations
follow from Eq. (20) and (21) by noting
that the spin harmonics are orthogonal,
.The gravitational sources and scattering sources of these equations
follow from Eq. (20) and (21) by noting
that the spin harmonics are orthogonal,
|  |
(26) |
The term  is evaluated by use of the coupling relation
Eq. (25) for
is evaluated by use of the coupling relation
Eq. (25) for 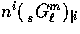 .It represents the fact that spatial gradients in the distribution become
orbital angular momentum as the radiation streams along its trajectory
.It represents the fact that spatial gradients in the distribution become
orbital angular momentum as the radiation streams along its trajectory
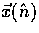 .For example, a temperature variation on a distant surface surrounding the
observer appears as an anisotropy on the sky.
This process then simply reflects a projection relation that relates distant
sources to present day local anisotropies.
.For example, a temperature variation on a distant surface surrounding the
observer appears as an anisotropy on the sky.
This process then simply reflects a projection relation that relates distant
sources to present day local anisotropies.
With these considerations, the temperature fluctuation evolves as
| 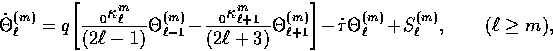 |
(27) |
and the polarization as
The temperature fluctuation sources in Newtonian gauge are
| 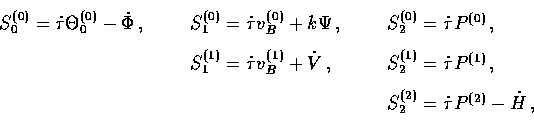 |
(28) |
and in synchronous gauge,
| 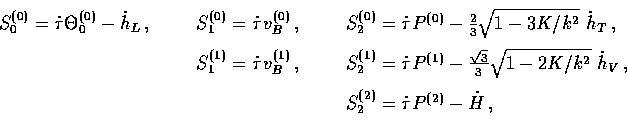 |
(29) |
The 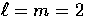 source doesn't contain a curvature factor because we have
recursively defined the basis functions in terms of the lowest member,
which is
source doesn't contain a curvature factor because we have
recursively defined the basis functions in terms of the lowest member,
which is 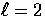 in this case. In the above
in this case. In the above
| ![\begin{displaymath}
P^{(m)} = {1 \over 10} \left[ \Theta_2^{(m)} - \sqrt{6} E_2^{(m)} \right].\end{displaymath}](img101.gif) |
(30) |
and note that the photon density and velocities are related to the 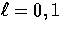 moments as
moments as
|  |
(31) |
whereas the anisotropic stresses are given by
| 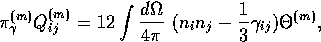 |
(32) |
which relates them to the quadrupole moments (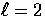 ) as
) as
| 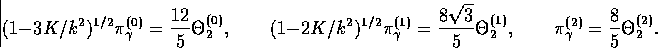 |
(33) |
The evolution of the metric and matter sources are given in
Appendices A3--A5.




Next: Integral Solutions
Up: Boltzmann Equation
Previous: Normal Modes
Wayne Hu
9/9/1997
![]() .The gravitational sources and scattering sources of these equations
follow from Eq. (20) and (21) by noting
that the spin harmonics are orthogonal,
.The gravitational sources and scattering sources of these equations
follow from Eq. (20) and (21) by noting
that the spin harmonics are orthogonal,
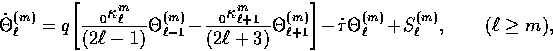
![\begin{displaymath}
\begin{array}
{rcl}\dot E_\ell^{(m)} &=&
q
\Bigg[ {\, {}_{...
...}
B_{\ell + 1}^{(m)} \Bigg] -\dot\tau B_\ell^{(m)}.\end{array}\end{displaymath}](img96.gif)