Integral Solutions

  The Boltzmann equations have formal integral solutions that are simple to write down. The hierarchy equations for the temperature distribution Eq. (33) merely express the projection of the various plane wave temperature sources $S_\ell^{(m)} \, {}_{0}^{\vphantom{m}} G_{\ell}^{m}$ on the sky today (see Eq. (36)). Likewise Eq. (34) expresses the projection of $-\sqrt{6} P^{(m)} \dot\tau e^{-\tau} \, {}_{\pm 2}^{\vphantom{m}} {G}_{\ell}^{m}$.

The projection is obtained by separating the total angular dependence of the mode from its decomposition in spherical coordinates: i.e. into radial functions times spin harmonics $\, {}_{s}^{\vphantom{m}} {Y}_{\ell}^{m}$.We discuss their explicit construction in Appendix B. The full solution immediately follows by integrating the projected source over the radial coordinate, 

$$\begin{array} {rcl}{\Theta_\ell^{(m)}(\eta_0,q) \over 2\ell ... ...6} P^{(m)}_{\vphantom{\ell}}) \,\beta_{\ell}^{(m)} ,\end{array}$$

where the arguments of the radial functions ($\phi_\ell,\epsilon_\ell,\beta_\ell$) are the distance to the source $\chi = \sqrt{-K}(\eta_0-\eta)$ and the reduced wavenumber $\nu=q/\sqrt{-K}$ (see Appendix B for explicit forms).

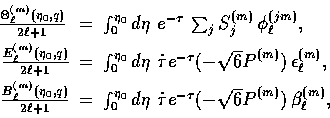The interpretation of these equations is also readily apparent from their form and construction. The decomposition of $\, {}_{s}^{\vphantom{m}} {G}_{j}^{m}$ into radial and spherical parts encapsulates the summation of spin and orbital angular momentum as well as the geodesic deviation factors described in §IIIB. The difference between the integral solution and the differential form is that in the former case the coupling is performed in one step from the source at time $\eta$ and distance $\chi(\eta)$ to the present, while in the latter the power is steadily transferred to higher $\ell$ as the time advances.

Take the flat space case. The intrinsic local angular momentum at the point $(\chi,\hat{n})$ is $\, {}_{s}^{\vphantom{m}} {Y}_{j}^{m}$ but must be added to the orbital angular momentum from the plane wave which can be expanded in terms of $j_\ell Y_\ell^0$.The result is a sum of $\vert\ell-j\vert$ to $\ell+j$ angular momentum states with weights given by Clebsch-Gordan coefficients. Alternately a state of definite angular momentum involves a sum over the same range in the spherical Bessel function. These linear combinations of Bessel functions are exactly the radial functions in Eq. (41) for the flat limit [1].

For an open geometry, the same analysis follows save that the spherical Bessel function must be replaced by a hyperspherical Bessel function (also called ultra-spherical Bessel functions) in the manner described in Appendix B. The qualitative aspect of this modification is clear from considering the angular diameter distance arguments of §IIIB. The peak in the Bessel function picks out the angle which a scale $k^{-1} \approx \sqrt{-K}\nu^{-1}$ subtends at distance $d \approx \chi/\sqrt{-K}$.A spherical Bessel function peaks when its argument $kd \approx \ell$or $\lambda/d \approx \theta$ in the small angle approximation. The hyperspherical Bessel function peaks at $k{\cal D}=\nu\sinh\chi \approx \ell$ for $\nu \gg 1$ or $\lambda/{\cal D} \approx \theta$ in the small angle approximation. The main effect of spatial curvature is simply to shift features in $\ell$-space with the angular diameter distance, i.e. to higher $\ell$or smaller angles in open universes. Similar arguments hold for closed geometries [16]. By virtue of this fact the division of polarization into E and B-modes remains the same as that in flat space. More specifically, for a single mode the ratio in power is given by  

$${\sum_\ell [\ell \beta_\ell^{(m)} ]^2 \over \sum_\ell [\ell... ...\cr 6, & $m= \pm 1,$\space \cr 8/13, & $m= \pm 2,$\space \cr}$$ (34)

at fixed source distance $\chi$ with $\nu \sin_K \chi \gg 1$.

The integral solutions (41) are the basis of the ``line of sight'' method [5,13] for rapid numerical calculation of CMB spectra, which has been employed in CMBFAST. The numerical implementation of equations (41) requires an efficient way of calculating the radial functions ($\phi_\ell,\epsilon_\ell,\beta_\ell$). This is best done acting the derivatives of the hyperspherical Bessel function in the radial equations (B3)-(B5) and (B11) on the sources through integration by parts. The remaining integrals can be efficiently calculated with the techniques of [4] for generating hyperspherical Bessel functions. The tensor CMBFAST code has now been modified to use the formalism described in this paper and the results have been cross-checked against solutions of the Boltzmann hierarchy equations (33)-(34) with very good agreement.