



Next: Evolution Equations
Up: Boltzmann Equation
Previous: Metric and Scattering Sources
The temperature and polarization distributions are functions of the position
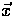 and the direction of propagation of the photons
and the direction of propagation of the photons 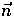 .
They can be expanded in modes which account for both the local angular and
spatial variations:
.
They can be expanded in modes which account for both the local angular and
spatial variations: 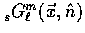 , i.e.
, i.e.
| 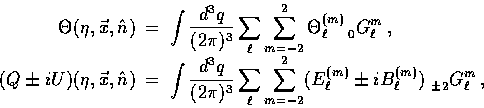 |
(18) |
with spin s=0 describing the temperature fluctuation and 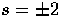 describing the polarization tensor.
describing the polarization tensor.
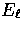 and
and 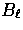 are the angular moments of the electric and magnetic
polarization components.
It is apparent that the effects of the local scattering process
are the angular moments of the electric and magnetic
polarization components.
It is apparent that the effects of the local scattering process 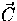 is most simply evaluated in a representation where the separation of the
local angular and spatial distribution is explicit [1], with the
former being an expansion in
is most simply evaluated in a representation where the separation of the
local angular and spatial distribution is explicit [1], with the
former being an expansion in 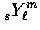 .The subtlety lies in relating the local basis at two different
coordinate points, say the last scattering event and the observer.
.The subtlety lies in relating the local basis at two different
coordinate points, say the last scattering event and the observer.
In flat space, the representation is straightforward since the parallel
transport of the angular basis in space is trivial. The result is a product
of spin-weighted harmonics for the local angular dependence and plane waves
for the spatial dependence:
| ![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(\vec{x},\hat{n}) =
(-...
...^{m}(\hat{n})] \exp(i\vec{k} \cdot \vec{x})\,,
\qquad (K=0)\,.\end{displaymath}](img72.gif) |
(19) |
Here we seek a similar construction in an curved geometry.
We will see that this construction greatly simplifies the scalar harmonic
treatment of [15,16,4] and extends it to vector and
tensor temperature [3] modes as well as all polarization modes.
To generalize these modes to the curved geometry, we wish to replace the
plane wave with some spatially dependent phase factor
![$\exp[i \delta(\vec{x},\vec{k})]$](img73.gif) related to the eigenfunctions
related to the eigenfunctions
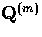 of §IIA while keeping the same local
angular dependence (see Eq. C2).
By virtue of this requirement, the Compton scattering terms, which
involve only the local angular dependence, retain the same form as in
flat space.
In Appendix C, we derive
of §IIA while keeping the same local
angular dependence (see Eq. C2).
By virtue of this requirement, the Compton scattering terms, which
involve only the local angular dependence, retain the same form as in
flat space.
In Appendix C, we derive 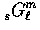 by
recursion from covariant contractions of the fundamental basis
by
recursion from covariant contractions of the fundamental basis 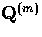 .The result is a recursive definition of the basis
.The result is a recursive definition of the basis
| 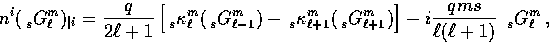 |
(20) |
constructed from the lowest 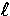 -mode of Eq. (B2)
with the coupling coefficient
-mode of Eq. (B2)
with the coupling coefficient
| ![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} {\kappa}_{\ell}^{m} = \sqrt{ \left[...
...s^2)\over\ell^2}\right]
\left[1 - {\ell^2\over q^2} K \right]}.\end{displaymath}](img77.gif) |
(21) |
The structure of this relation is readily apparent. The recursion relation
expresses the addition of angular momentum and is the defining equation in
the total angular momentum method.
It says the ``total'' local angular dependence at (say) the origin is the
sum of the local angular dependence at distant points (``spin'' angular
momentum) plus the angular variations induced by the spatial dependence of
the mode (``orbital'' angular momentum).
The recursion relation represents the addition of angular momentum for the
case of an infinitesimal spatial separation.
Here the leading order spatial variation is the gradient
[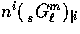 ]
term which has an angular structure of a dipole Y10.
The first term on the rhs of equation (26) arises from the
Clebsch-Gordan relation that couples the orbital Y10 with the intrinsic
]
term which has an angular structure of a dipole Y10.
The first term on the rhs of equation (26) arises from the
Clebsch-Gordan relation that couples the orbital Y10 with the intrinsic
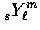 to form
to form 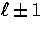 states,
states,
| 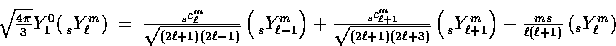 |
(22) |
where the coupling coefficient is 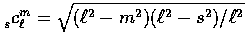 .
.
The second term on the rhs of the coupling equation (26)
accounts for geodesic deviation factors in the conversion of spatial
structure into orbital angular momentum.
Consider first a closed universe with radius of curvature 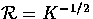 .Suppressing one spatial coordinate, we can analyze the problem as geometry on
the 2-sphere with the observer situated at the pole.
Light travels on radial geodesics or great circles of fixed longitude.
A physical scale
.Suppressing one spatial coordinate, we can analyze the problem as geometry on
the 2-sphere with the observer situated at the pole.
Light travels on radial geodesics or great circles of fixed longitude.
A physical scale 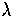 at fixed latitude (given by the polar angle
at fixed latitude (given by the polar angle 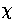 )subtends an angle
)subtends an angle 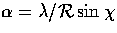 .In the small angle approximation, a Euclidean analysis would infer a distance
related by
.In the small angle approximation, a Euclidean analysis would infer a distance
related by
| 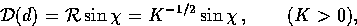 |
(23) |
called here the angular diameter distance.
For negatively curved or open universes, a similar analysis implies
| 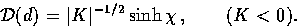 |
(24) |
Thus the angular scale corresponding to an eigenmode of
wavelength 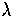 is
is
| 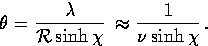 |
(25) |
For an infinitesimal change 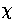 , orbital angular momentum
of order
, orbital angular momentum
of order 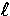 is stimulated when
which explains the factors of
is stimulated when
which explains the factors of 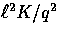 in the coupling term in a
curved geometry.
We shall see in §IIID that these infinitesimal additions of
angular momentum and geodesic deviation may be encorporated into a single
step by finding the integral solutions to the coupling equation
(25).
in the coupling term in a
curved geometry.
We shall see in §IIID that these infinitesimal additions of
angular momentum and geodesic deviation may be encorporated into a single
step by finding the integral solutions to the coupling equation
(25).




Next: Evolution Equations
Up: Boltzmann Equation
Previous: Metric and Scattering Sources
Wayne Hu
9/9/1997
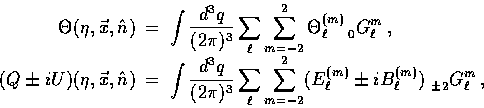
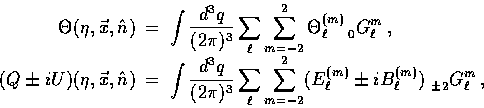
![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} G_{\ell}^{m}(\vec{x},\hat{n}) =
(-...
...^{m}(\hat{n})] \exp(i\vec{k} \cdot \vec{x})\,,
\qquad (K=0)\,.\end{displaymath}](img72.gif)
![]() related to the eigenfunctions
related to the eigenfunctions
![]() of §IIA while keeping the same local
angular dependence (see Eq. C2).
By virtue of this requirement, the Compton scattering terms, which
involve only the local angular dependence, retain the same form as in
flat space.
In Appendix C, we derive
of §IIA while keeping the same local
angular dependence (see Eq. C2).
By virtue of this requirement, the Compton scattering terms, which
involve only the local angular dependence, retain the same form as in
flat space.
In Appendix C, we derive ![]() by
recursion from covariant contractions of the fundamental basis
by
recursion from covariant contractions of the fundamental basis ![]() .The result is a recursive definition of the basis
.The result is a recursive definition of the basis
![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} {\kappa}_{\ell}^{m} = \sqrt{ \left[...
...s^2)\over\ell^2}\right]
\left[1 - {\ell^2\over q^2} K \right]}.\end{displaymath}](img77.gif)
![]() ]
term which has an angular structure of a dipole Y10.
The first term on the rhs of equation (26) arises from the
Clebsch-Gordan relation that couples the orbital Y10 with the intrinsic
]
term which has an angular structure of a dipole Y10.
The first term on the rhs of equation (26) arises from the
Clebsch-Gordan relation that couples the orbital Y10 with the intrinsic
![]() to form
to form ![]() states,
states,
![]() .Suppressing one spatial coordinate, we can analyze the problem as geometry on
the 2-sphere with the observer situated at the pole.
Light travels on radial geodesics or great circles of fixed longitude.
A physical scale
.Suppressing one spatial coordinate, we can analyze the problem as geometry on
the 2-sphere with the observer situated at the pole.
Light travels on radial geodesics or great circles of fixed longitude.
A physical scale ![]() at fixed latitude (given by the polar angle
at fixed latitude (given by the polar angle ![]() )subtends an angle
)subtends an angle ![]() .In the small angle approximation, a Euclidean analysis would infer a distance
related by
.In the small angle approximation, a Euclidean analysis would infer a distance
related by
![\begin{displaymath}
\begin{array}
{rcl}\chi &\approx& {1\over\nu\theta} [1+{\cal...
...pprox& {\ell\over q}[1+{\cal O}(\ell^2 K / q^2) ]\,,\end{array}\end{displaymath}](img89.gif)