



Next: Derivation of the Normal
Up: A COMPLETE TREATMENT OF
Previous: Tensor Einstein Equations
It often useful to represent the eigenmodes
in a spherical coordinate system 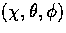 where
where 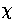 is the radial coordinate scaled to the curvature radius. Here we
explicitly write down the forms and properties of the radial
modes in an open geometry and describe the modifications
necessary to treat closed geometries.
is the radial coordinate scaled to the curvature radius. Here we
explicitly write down the forms and properties of the radial
modes in an open geometry and describe the modifications
necessary to treat closed geometries.
By separation of variables in the Laplacian, we can write
| 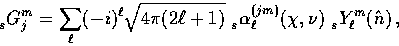 |
(50) |
and the goal is to find explicit expressions for
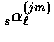 . Here the
. Here the 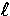 -weights are set to reproduce
the flat space conventions of spherical Bessel functions (see also [1]).
We proceed by analyzing the lowest
-weights are set to reproduce
the flat space conventions of spherical Bessel functions (see also [1]).
We proceed by analyzing the lowest 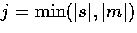 harmonic
where
harmonic
where 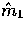 and
and 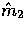 form a right-handed orthonormal
basis with
form a right-handed orthonormal
basis with 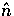 .We can now determine
.We can now determine 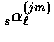 from
the radial representation of
from
the radial representation of 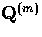 [18]
for
[18]
for 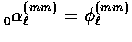 ;similarly for
;similarly for
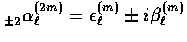 ,
and
for m > 0. For m<0,
,
and
for m > 0. For m<0, 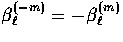 while the other
two functions remain the same.
Here
while the other
two functions remain the same.
Here 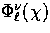 is the hyperspherical Bessel function
whose properties are discussed extensively by [6].
is the hyperspherical Bessel function
whose properties are discussed extensively by [6].
The overall normalization of the modes here has been altered from those of
[6,18] in the case of vector and tensor temperature modes such that
| 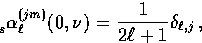 |
(51) |
where the difference lies in the lack of curvature dependence in the relation.
Our choice simplifies the equations since it preserves the flat space form of
the equations locally around the origin.
It also defines the normalization of the polarization modes with
respect to Qij(m) through Eq. (B2).
The properties of the hyperspherical Bessel functions imply useful properties
for the radial functions.
For our purposes, the important relations they obey are:
which define the series in terms of its first member
| 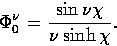 |
(52) |
Notice that 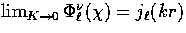 .
.
From the recursion relations of 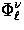 one establishes
the corresponding relations for the radial function
one establishes
the corresponding relations for the radial function
| ![\begin{displaymath}
{d \over d\chi} [\, {}_{s}^{\vphantom{(j m)}} {\alpha}_{\ell...
...\, {}_{s}^{\vphantom{(j m)}} {\alpha}_{\ell}^{(j m)}\right]\, ,\end{displaymath}](img204.gif) |
(53) |
for the lowest j, where recall
| ![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} {\kappa}_{\ell}^{m}
=\sqrt{\left[ ...
...)\over \ell^2}\right]
\left[ 1+{\ell^2\over\nu^2}\right] }\, . \end{displaymath}](img205.gif) |
(54) |
The construction of the higher 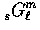 via
the recursion relation of Eq. (25) also returns
the higher radial harmonics. A few useful ones are
via
the recursion relation of Eq. (25) also returns
the higher radial harmonics. A few useful ones are
Furthermore, the recursion relation obeyed by the higher radial harmonics
is the same as Eq. (B9), by virtue of
Eq. (C5) and explicit substitution of the radial form
Eq. (C3).
This j-independence of the recursion relation implies that
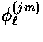 is a solution to the temperature hierarchy
Eq. (33) for any j and aids in the construction of
the integral solutions in §IIID.
is a solution to the temperature hierarchy
Eq. (33) for any j and aids in the construction of
the integral solutions in §IIID.
Finally, the radial functions for a closed geometry follow by replacing
all 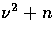 , where n is integer, with
, where n is integer, with 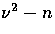 and trigonometric
functions with hyperbolic trigonometric functions (see [6,18] for
details).
and trigonometric
functions with hyperbolic trigonometric functions (see [6,18] for
details).




Next: Derivation of the Normal
Up: A COMPLETE TREATMENT OF
Previous: Tensor Einstein Equations
Wayne Hu
9/9/1997
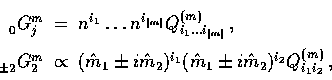
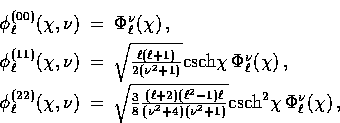
![\begin{displaymath}
\begin{array}
{rcl}\epsilon_{\ell}^{(0)}(\chi,\nu)
& = & \sq...
...coth}^2 \chi \right) \Phi_\ell^\nu(\chi)
\right]\,,\end{array}\end{displaymath}](img195.gif)
![\begin{displaymath}
\begin{array}
{rcl}\beta_{\ell}^{(0)}(\chi,\nu) &=& 0 \,, \n...
...(\chi)+2{\rm coth}\chi\Phi_\ell^\nu(\chi) \right]\,,\end{array}\end{displaymath}](img196.gif)
![\begin{displaymath}
\begin{array}
{rcl}{d \over d\chi}\Phi_\ell^\nu& = &
{1 \ove...
...sqrt{\nu^2 + (\ell+1)^2} \Phi_{\ell+1}^\nu\right]\,,\end{array}\end{displaymath}](img200.gif)
![]() one establishes
the corresponding relations for the radial function
one establishes
the corresponding relations for the radial function
![\begin{displaymath}
\, {}_{s}^{\vphantom{m}} {\kappa}_{\ell}^{m}
=\sqrt{\left[ ...
...)\over \ell^2}\right]
\left[ 1+{\ell^2\over\nu^2}\right] }\, . \end{displaymath}](img205.gif)
![]() via
the recursion relation of Eq. (25) also returns
the higher radial harmonics. A few useful ones are
via
the recursion relation of Eq. (25) also returns
the higher radial harmonics. A few useful ones are
![\begin{displaymath}
\begin{array}
{rcl}\phi_{\ell}^{(10)}(\chi,\nu)
& = & \sqrt{...
...eft[ {\rm csch}\chi \Phi_\ell^\nu(\chi) \right]' \,.\end{array}\end{displaymath}](img206.gif)
![]() , where n is integer, with
, where n is integer, with ![]() and trigonometric
functions with hyperbolic trigonometric functions (see [6,18] for
details).
and trigonometric
functions with hyperbolic trigonometric functions (see [6,18] for
details).