



Next: Free Streaming
Up: Evolution Equations
Previous: Evolution Equations
The temperature and polarization fluctuations
are expanded into the normal modes defined
in §IIB,![[*]](foot_motif.gif)
| 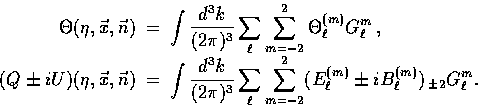 |
(47) |
A comparison with Eqn. (9) and
(43) shows
that 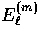 and
and 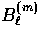 represent
polarization with electric
represent
polarization with electric 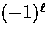 and magnetic
and magnetic 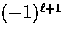 type parities
respectively [3,4]. Because the temperature
type parities
respectively [3,4]. Because the temperature
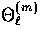 has electric type parity, only
has electric type parity, only 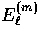 couples
directly to the temperature in the scattering sources.
Note that
couples
directly to the temperature in the scattering sources.
Note that 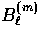 and
and 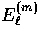 represent polarizations
with Q and U interchanged and thus represent polarization
patterns rotated by
represent polarizations
with Q and U interchanged and thus represent polarization
patterns rotated by 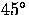 . A simple example is given by
the m=0 modes. In the
. A simple example is given by
the m=0 modes. In the 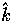 -frame,
-frame,
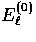 represents a pure Q,
or north/south-east/west, polarization field
whose amplitude depends on
represents a pure Q,
or north/south-east/west, polarization field
whose amplitude depends on
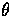 , e.g.
, e.g. 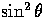 for
for 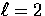 .
. 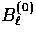 represents a pure U, or northwest/southeast-northeast/southwest,
polarization with the
same dependence.
represents a pure U, or northwest/southeast-northeast/southwest,
polarization with the
same dependence.
The power spectra of temperature and polarization anisotropies
today are defined as, e.g. 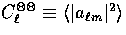 for
for 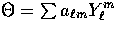 with the average being over
the (
with the average being over
the (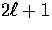 ) m-values. Recalling the normalization of the
mode functions from Eqn. (10) and
(11), we obtain
) m-values. Recalling the normalization of the
mode functions from Eqn. (10) and
(11), we obtain
| 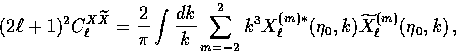 |
(48) |
where X takes on the values 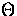 , E and B.
There is no cross correlation
, E and B.
There is no cross correlation 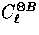 or
or
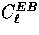 due to parity [see Eqns. (6) and
(24)].
We also employ the notation
due to parity [see Eqns. (6) and
(24)].
We also employ the notation 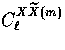 for the m contributions
individually.
Note that
for the m contributions
individually.
Note that 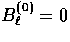 here due to
azimuthal symmetry in the transport problem so that
here due to
azimuthal symmetry in the transport problem so that 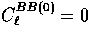 .
.
As we shall now show, the 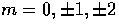 modes are stimulated by
scalar, vector and tensor perturbations in the metric. The
orthogonality of the spherical harmonics assures us that these modes
are independent, and we now discuss the contributions separately.
modes are stimulated by
scalar, vector and tensor perturbations in the metric. The
orthogonality of the spherical harmonics assures us that these modes
are independent, and we now discuss the contributions separately.




Next: Free Streaming
Up: Evolution Equations
Previous: Evolution Equations
Wayne Hu
9/9/1997
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
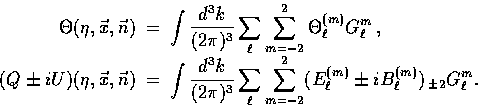
![]() for
for ![]() with the average being over
the (
with the average being over
the (![]() ) m-values. Recalling the normalization of the
mode functions from Eqn. (10) and
(11), we obtain
) m-values. Recalling the normalization of the
mode functions from Eqn. (10) and
(11), we obtain
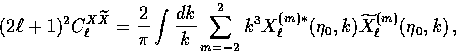
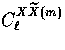 for the m contributions
individually.
Note that
for the m contributions
individually.
Note that ![]() modes are stimulated by
scalar, vector and tensor perturbations in the metric. The
orthogonality of the spherical harmonics assures us that these modes
are independent, and we now discuss the contributions separately.
modes are stimulated by
scalar, vector and tensor perturbations in the metric. The
orthogonality of the spherical harmonics assures us that these modes
are independent, and we now discuss the contributions separately.