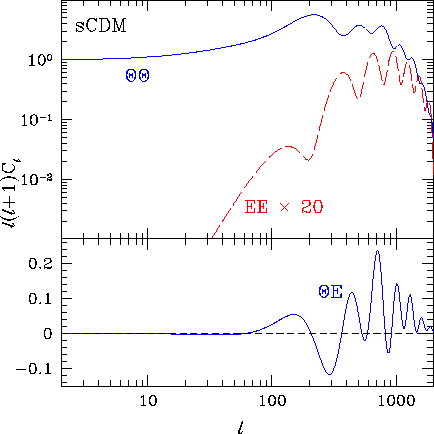
Figure 6:
Power spectra for the standard cold dark matter
model (scale invariant scalar adiabatic initial conditions with
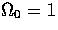 , h=0.5 and
, h=0.5 and 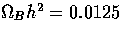 ). Notice that
B-polarization is absent, E-polarization scales as
). Notice that
B-polarization is absent, E-polarization scales as 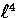 at large angles and the cross correlation (
at large angles and the cross correlation (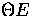 )is negative at large
angles and reflects the acoustic oscillations at small angles.
In particular the phase of the EE and
)is negative at large
angles and reflects the acoustic oscillations at small angles.
In particular the phase of the EE and 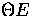 acoustic peaks is set by the temperature oscillations
acoustic peaks is set by the temperature oscillations 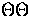 (see §IVB).
(see §IVB).
 |
These scaling relations
between the metric and anisotropic
scattering sources of the temperature and polarization are important
for understanding the large angle behavior of the polarization and
temperature polarization cross spectrum. Here last scattering
is effectively instantaneous compared with the scale of the
perturbation and the tight coupling remains a good approximation
through last scattering.
For the scalars, the Euler equation (80)
may be used to express the scalar velocity and hence the
polarization in terms of
the effective temperature,
| 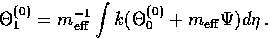 |
(73) |
Since 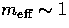 ,
,
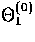 has the same sign as
has the same sign as 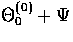 before
before 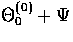 itself can change
signs,
assuming reasonable initial conditions.
It then follows that P(0) is also of the same sign
and is of order
itself can change
signs,
assuming reasonable initial conditions.
It then follows that P(0) is also of the same sign
and is of order
| ![\begin{displaymath}
P^{(0)} \sim (k\eta){k \over \dot\tau} [\Theta_0^{(0)}+ \Psi]\, ,\end{displaymath}](img351.gif) |
(74) |
which is strongly suppressed for 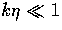 .
The definite sign leads to a definite prediction
for the sign of the temperature polarization cross correlation
on large angles.
.
The definite sign leads to a definite prediction
for the sign of the temperature polarization cross correlation
on large angles.
For the vectors
|  |
(75) |
and is both suppressed and has a definite sign
in relation to the metric fluctuation. The tensor relation
to the metric is given in Eqn. (90).
In fact, in all three cases the dominant
source of temperature perturbations has the same sign as
the anisotropic scattering source P(m). From
Eqn. (79), differences in the
sense of the
cross correlation between temperature and polarization thus
arise only due to geometric reasons in the projection
of the sources
(see Fig. 5). On angles larger than the
horizon at last scattering, the scalar and vector 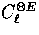 is negative whereas the tensor cross power is positive
[9,21].
is negative whereas the tensor cross power is positive
[9,21].
On smaller scales, the scalar polarization follows the velocity
in the tight coupling regime. It is instructive to recall the
solutions for the acoustic oscillations from
Eqn. (83). The velocity oscillates  out of phase with the temperature and hence the E-polarization
acoustic peaks will be out of phase with the temperature
peaks (see Fig. 6). The cross correlation oscillates
as
out of phase with the temperature and hence the E-polarization
acoustic peaks will be out of phase with the temperature
peaks (see Fig. 6). The cross correlation oscillates
as 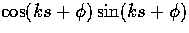 and hence has twice the
frequency. Thus between peaks of the polarization and temperature
power spectra (which represents both peaks and troughs of
the temperature amplitude) the cross correlation
peaks. The structure of the cross correlation
can be used to measure the acoustic phase
and hence has twice the
frequency. Thus between peaks of the polarization and temperature
power spectra (which represents both peaks and troughs of
the temperature amplitude) the cross correlation
peaks. The structure of the cross correlation
can be used to measure the acoustic phase 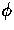 (
(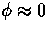 for adiabatic models) and how
it changes with scale just as the temperature but like the EE
power spectrum [27] has the added
benefit of probing slightly larger scales than
the first temperature peak.
This property can help distinguish adiabatic
and isocurvature models due to causal constraints on
the generation of acoustic waves at the horizon at last scattering
[28].
for adiabatic models) and how
it changes with scale just as the temperature but like the EE
power spectrum [27] has the added
benefit of probing slightly larger scales than
the first temperature peak.
This property can help distinguish adiabatic
and isocurvature models due to causal constraints on
the generation of acoustic waves at the horizon at last scattering
[28].
Finally, polarization also increases the viscosity of the fluid
by a factor of 6/5, which has significant effects for the
temperature.
Even though the viscous imperfections of the fluid
are small in the tight coupling region they can lead to significant
dissipation of the fluctuations over time
(see §IVD).




Next: Entropy and Heat Conduction
Up: Photon-Baryon Fluid
Previous: Compression and Vorticity
Wayne Hu
9/9/1997

![]() out of phase with the temperature and hence the E-polarization
acoustic peaks will be out of phase with the temperature
peaks (see Fig. 6). The cross correlation oscillates
as
out of phase with the temperature and hence the E-polarization
acoustic peaks will be out of phase with the temperature
peaks (see Fig. 6). The cross correlation oscillates
as ![]() and hence has twice the
frequency. Thus between peaks of the polarization and temperature
power spectra (which represents both peaks and troughs of
the temperature amplitude) the cross correlation
peaks. The structure of the cross correlation
can be used to measure the acoustic phase
and hence has twice the
frequency. Thus between peaks of the polarization and temperature
power spectra (which represents both peaks and troughs of
the temperature amplitude) the cross correlation
peaks. The structure of the cross correlation
can be used to measure the acoustic phase ![]() (
(![]() for adiabatic models) and how
it changes with scale just as the temperature but like the EE
power spectrum [27] has the added
benefit of probing slightly larger scales than
the first temperature peak.
This property can help distinguish adiabatic
and isocurvature models due to causal constraints on
the generation of acoustic waves at the horizon at last scattering
[28].
for adiabatic models) and how
it changes with scale just as the temperature but like the EE
power spectrum [27] has the added
benefit of probing slightly larger scales than
the first temperature peak.
This property can help distinguish adiabatic
and isocurvature models due to causal constraints on
the generation of acoustic waves at the horizon at last scattering
[28].