



Next: Scaling Stress Seeds
Up: Photon-Baryon Fluid
Previous: Entropy and Heat Conduction
The generation of viscosity and heat conduction in the fluid
dissipates fluctuations through the Euler equations
with (89)
and (94),
where we have dropped the 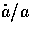 factors under the assumption
that the expansion can be neglected
during the dissipation period. We have also employed
Eqn. (85) to
eliminate higher order terms in the
vector equation. With the continuity equation for the
scalars
factors under the assumption
that the expansion can be neglected
during the dissipation period. We have also employed
Eqn. (85) to
eliminate higher order terms in the
vector equation. With the continuity equation for the
scalars 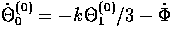 (see Eqn. 60
(see Eqn. 60 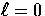 , m=0 ), we obtain
, m=0 ), we obtain
| 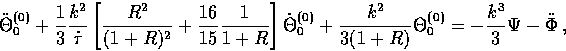 |
(76) |
which is a damped forced oscillator equation.
An interesting case to consider is the behavior in the absence
of metric fluctuations 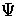 ,
, 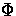 , and V. The result,
immediately apparent from Eqn. (96) and
(97), is that
the acoustic amplitude (m=0) and vorticity (m=1) damp as
, and V. The result,
immediately apparent from Eqn. (96) and
(97), is that
the acoustic amplitude (m=0) and vorticity (m=1) damp as
![$\exp[-(k/k_D^{(m)})^2]$](img367.gif) where
where
Notice that dissipation is less rapid for the vectors
compared with the scalars once
the fluid becomes baryon dominated 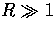 because of the
absence of heat conduction damping. In principle, this allows
vectors to contribute more CMB anisotropies at small scales
due to fluid contributions. In practice, the dissipative cut off
scales are not very far apart since
because of the
absence of heat conduction damping. In principle, this allows
vectors to contribute more CMB anisotropies at small scales
due to fluid contributions. In practice, the dissipative cut off
scales are not very far apart since 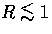 at recombination.
at recombination.
Vectors may also dominate if there is a continual metric
source. There is a competition between the metric source
and dissipational sinks in Eqns. (96) and
(97). Scalars retain contributions
to 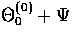 of
of
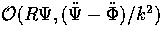 (see Eqn. (84) and [29]).
The vector solution becomes
(see Eqn. (84) and [29]).
The vector solution becomes
| ![\begin{displaymath}
\Theta_1^{(1)}(\eta) = e^{-[k/k_D^{(1)}(\eta)]^2}
\int_0^\eta d\eta' \dot V
e^{[k/{k_D^{(1)}}(\eta')]^2} ,\end{displaymath}](img373.gif) |
(77) |
which says that if variations in the metric are rapid compared with
the damping then 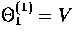 and damping does not occur.
and damping does not occur.




Next: Scaling Stress Seeds
Up: Photon-Baryon Fluid
Previous: Entropy and Heat Conduction
Wayne Hu
9/9/1997
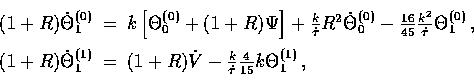
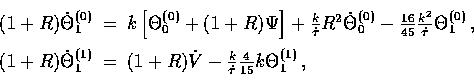
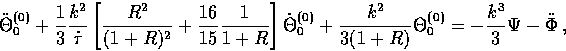
![]() ,
, ![]() , and V. The result,
immediately apparent from Eqn. (96) and
(97), is that
the acoustic amplitude (m=0) and vorticity (m=1) damp as
, and V. The result,
immediately apparent from Eqn. (96) and
(97), is that
the acoustic amplitude (m=0) and vorticity (m=1) damp as
![]() where
where
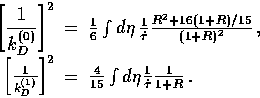
![]() of
of
![]() (see Eqn. (84) and [29]).
The vector solution becomes
(see Eqn. (84) and [29]).
The vector solution becomes