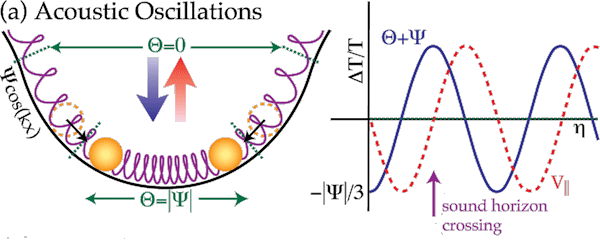
Since the turning points of the oscillation are at the extrema, the fluid oscillates 90 degrees out of phase with the temperature. Its line-of-sight motion relative to the observer causes a Doppler shift.
Figure: Doppler Effect (in red)
If the baryons are neglected, the Doppler oscillations have the same amplitude as the temperature oscillations. However, as we have seen, baryons increase both the amplitude of the oscillation and the rms magnitude of the compressional peaks strongly. Furthermore, by conservation of energy, as the effective mass of the oscillator goes up, the velocity goes down as the square root of the mass. Together, these factors imply that in the real universe which has a significant baryon content, the Doppler effect is subdominant.
Figure: Relative Suppression by Baryons
An analytic decomposition of the anisotropy shows this effect clearly.
Figure: Decomposition from based on Hu &White (1997)
The total contribution includes damping processses and ISW effects.
The Doppler effect plays a more significant role if the universe is reionized.