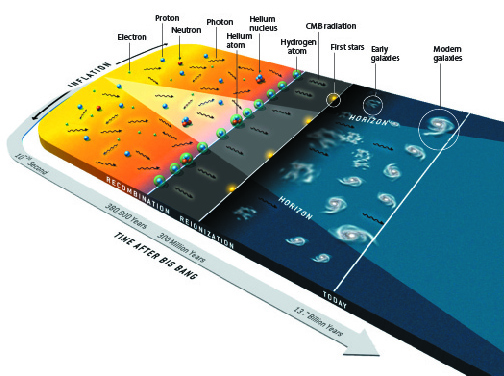
In the beginning, there was light. Under the intense conditions of the early universe, ionized matter gave off radiation that was trapped within it like light in a dense fog. But as the universe expanded and cooled, electrons and protons came together to form neutral atoms, and matter lost its ability to ensnare light. Today, some 14 billion years later, the photons from that great release of radiation form the cosmic microwave background (CMB).
Tune a television set between channels, and about 1 percent of the static you see on the screen is from the CMB. When astronomers scan the sky for these microwaves, they find that the signal looks almost identical in every direction. The ubiquity and constancy of the CMB is a sign that it comes from a simpler past, long before structures such as planets, stars and galaxies formed. Because of this simplicity, we can predict the properties of the CMB to exquisite accuracy. And in the past few years, cosmologists have been able to compare these predictions with increasingly precise observations from microwave telescopes carried by balloons and spacecraft. This research has brought us closer to answering some age-old questions: What is the universe made of? How old is it? And where did objects in the universe, including our planetary home, come from?
Arno Penzias and Robert Wilson of AT&T Bell Laboratories detected the CMB radiation in 1965 while trying to find the source of a mysterious background noise in their radio antenna. The discovery firmly established the big bang theory, which states that the early universe was a hot, dense plasma of charged particles and photons. Since that time, the CMB has been cooled by the expansion of the universe, and it is extremely cold today &mdash comparable to the radiation released by a body at a temperature of 2.7 kelvins (that is, 2.7 degrees Celsius above absolute zero). But when the CMB was released, its temperature was nearly 3,000 kelvins (or about 2,727 degrees C).
In 1990 a satellite called COBE (for Cosmic Background Explorer) measured the spectrum of the CMB radiation, showing it to have exactly the expected form. Overshadowing this impressive achievement, however, was COBE's detection of slight variations &mdash at the level of one part in 100,000 &mdash in the temperature of the CMB from place to place in the sky. Observers had been diligently searching for these variations for more than two decades because they hold the key to understanding the origin of structure in the universe: how the primordial plasma evolved into galaxies, stars and planets.
Since then, scientists have employed ever more sophisticated instruments to map the temperature variations of the CMB. The culmination of these efforts was the launch in 2001 of the Wilkinson Microwave Anisotropy Probe (WMAP), which travels around the sun in an orbit 1.5 million kilometers beyond Earth's. The results from WMAP reveal that the CMB temperature variations follow a distinctive pattern predicted by cosmological theory: the hot and cold spots in the radiation fall into characteristic sizes. What is more, researchers have been able to use these data to precisely estimate the age, composition and geometry of the universe. The process is analogous to determining the construction of a musical instrument by carefully listening to its notes. But the cosmic symphony is produced by some very strange players and is accompanied by even stranger coincidences that cry out for explanation.
Our basic understanding of the physics behind these observations dates back to the late 1960s, when P. James E. Peebles of Princeton University and graduate student Jer Yu realized that the early universe would have contained sound waves. (At almost the same time, Yakov B. Zel'dovich and Rashid A. Sunyaev of the Moscow Institute of Applied Mathematics were coming to very similar conclusions.) When radiation was still trapped by matter, the tightly coupled system of photons, electrons and protons behaved as a single gas, with photons scattering off electrons like ricocheting bullets. As in the air, a small disturbance in gas density would have propagated as a sound wave, a train of slight compressions and rarefactions. The compressions heated the gas and the rarefactions cooled it, so any disturbance in the early universe resulted in a shifting pattern of temperature fluctuations.
When distances in the universe grew to one thousandth of their current size — about 380,000 years after the big bang &mdash the temperature of the gas decreased enough for the protons to capture the electrons and become atoms. This transition, called recombination, changed the situation dramatically. The photons were no longer scattered by collisions with charged particles, so for the first time they traveled largely unimpeded through space. Photons released from hotter, denser areas were more energetic than photons emitted from rarefied regions, so the pattern of hot and cold spots induced by the sound waves was frozen into the CMB. At the same time, matter was freed of the radiation pressure that had resisted the contraction of dense clumps. Under the attractive influence of gravity, the denser areas coalesced into stars and galaxies. In fact, the one-in-100,000 variations observed in the CMB are of exactly the right amplitude to form the large-scale structures we see today.
Yet what was the prime mover, the source of the initial disturbances that triggered the sound waves? The question is troubling. Imagine yourself as an observer witnessing the big bang and the subsequent expansion. At any given point you will see only a finite region of the universe that encompasses the distance light has traveled since the big bang. Cosmologists call the edge of this region the horizon, the place beyond which you cannot see. This region continuously grows until it reaches the radius of the observable universe today. Because information cannot be conveyed faster than light, the horizon defines the sphere of influence of any physical mechanism. As we go backward in time to search for the origin of structures of a particular physical size, the horizon eventually becomes smaller than the structure. Therefore, no physical process that obeys causality can explain the structure's origin. In cosmology, this dilemma is known as the horizon problem.

As inflation expanded the universe, the plasma of photons and charged particles grew far beyond the horizon (the edge of the region that a hypothetical viewer after inflation would see as the universe expands). During the recombination period about 380,000 years later, the first atoms formed and the cosmic microwave background (CMB) radiation was emitted. After another 300 million years, radiation from the first stars reionized most of the hydrogen and helium.
Fortunately, the theory of inflation solves the horizon problem and also provides a physical mechanism for triggering the primordial sound waves and the seeds of all structure in the universe. The theory posits a new form of energy, carried by a field dubbed the inflation which caused an accelerated expansion of the universe in the very first moments after the big bang. As a result, the observable universe we see today is only a small fraction of the observable universe before inflation. Furthermore, quantum fluctuations in the inflaton field, magnified by the rapid expansion, provide initial disturbances that are approximately equal on all scales — that is, the disturbances to small regions have the same magnitude as those affecting large regions. These disturbances become fluctuations in the energy density from place to place in the primordial plasma. Evidence supporting the theory of inflation has now been found in the detailed pattern of sound waves in the CMB. Because inflation produced the density disturbances all at once in essentially the first moment of creation, the phases of all the sound waves were synchronized. The result was a sound spectrum with overtones much like a musical instrument's. Consider blowing into a pipe that is open at both ends. The fundamental frequency of the sound corresponds to a wave (also called a mode of vibration) with maximum air displacement at either end and minimum displacement in the middle.
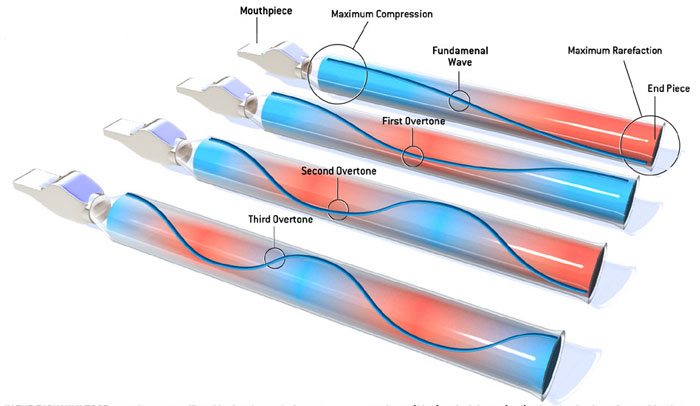
The sound spectrum of the early universe had overtones much like a musical instrument's. If you blow into a pipe, the sound corresponds to a wave with maximum air compression (blue) at the mouthpiece and maximum rarefaction (red) at the end piece. But the sound also has a series of overtones with shorter wavelengths that are integer fractions of the fundamental wavelength. (The wavelengths of the first, second and third overtones are one half, one third and one fourth as long.)
The wavelength of the fundamental mode is twice the length of the pipe. But the sound also has a series of overtones corresponding to wavelengths that are integer fractions of the fundamental wavelength: one half, one third, one fourth and so on. To put it another way, the frequencies of the overtones are two, three, four or more times as high as the fundamental frequency. Overtones are what distinguish a Stradivarius from an ordinary violin; they add richness to the sound.
The sound waves in the early universe are similar, except now we must imagine the waves oscillating in time instead of space In this analogy, the length of the pipe represents the finite duration when sound waves traveled through the primordial plasma; the waves start at inflation and end at recombination about 380,000 years later. Assume that a certain region of space has a maximum positive displacement — that is, maximum temperature &mdash at inflation. As the sound waves propagate, the density of the region will begin to oscillate, first heading toward average temperature (maximum negative displacement). The wave that causes the region to reach maximum negative displacement exactly at recombination is the fundamental wave of the early universe. The overtones have wavelengths that are integer fractions of the fundamental wavelength. Oscillating two, three or more times as quickly as the fundamental wave, these overtones cause smaller regions of space to reach maximum displacement, either positive or negative, at recombination.
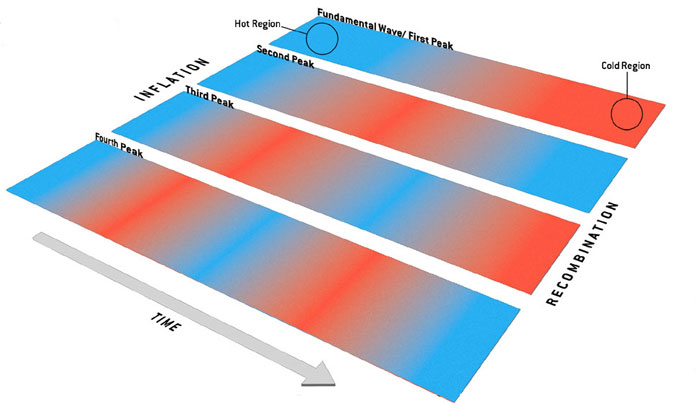
Sound waves also oscillated in the plasma of the early universe. After inflation, the fundamental wave compressed some regions of plasma and rarefied others, causing the temperature of the CMB radiation in the regions to reach maximum (blue) and minimum (red) values by the time of recombination. The overtones oscillated two, three or more times as quickly, causing smaller regions to reach maximum and minimum CMB temperatures at the time of recombination.
How do cosmologists deduce this pattern from the CMB? They plot the magnitude of the temperature variations against the sizes of the hot and cold spots in a graph called a power spectrum.
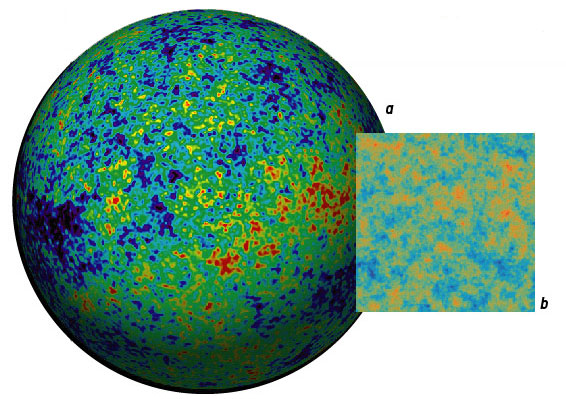
Observations of the CMB provide a map of temperature variations across the whole sky (a). When researchers analyze portions of that map (b), they use band filters to show how the temperature of the radiation varies at different scales.
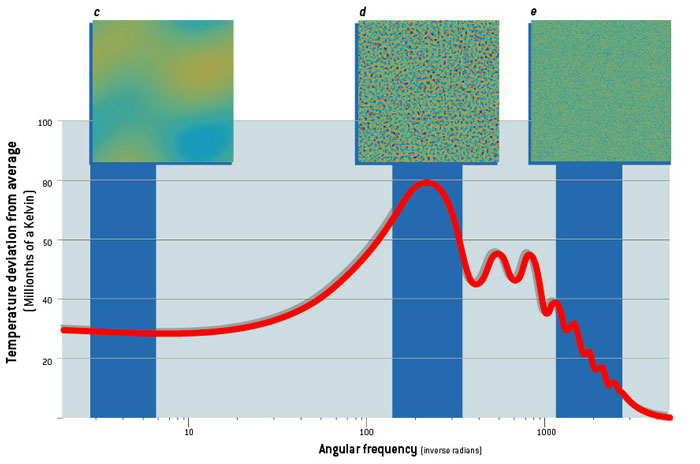
The variations are barely noticeable at large scales corresponding to regions that stretch about 30 degrees across the sky (c) and at small scales corresponding to regions about a tenth of a degree across (e). But the temperature differences are quite distinct for regions about one degree across (d). This first peak in the power spectrum (graph at bottom) reveals the compressions and rarefactions caused by the fundamental wave of the early universe; the subsequent peaks show the effects of the overtones.
Sound waves also oscillated in the plasma of the early universe. After inflation, the fundamental wave compressed some regions of plasma and rarefied others, causing the temperature of the CMB radiation in the regions to reach maximum (blue) and minimum (red) values by the time of recombination. The overtones oscillated two, three or more times as quickly, causing smaller regions to reach maximum and minimum CMB temperatures at the time of recombination. The results show that the regions with the greatest variations subtend about one degree across the sky, or nearly twice the size of the full moon. (At the time of recombination, these regions had diameters of about one million light-years, but because of the 1,000-fold expansion of the universe since then, each region now stretches nearly one billion light-years across.) This first and highest peak in the power spectrum is evidence of the fundamental wave, which compressed and rarefied the regions of plasma to the maximum extent at the time of recombination. The subsequent peaks in the power spectrum represent the temperature variations caused by the overtones. The series of peaks strongly supports the theory that inflation triggered all the sound waves at the same time. If the perturbations had been continuously generated over time, the power spectrum would not be so harmoniously ordered. To return to our pipe analogy, consider the cacophony that would result from blowing into a pipe that has holes drilled randomly along its length.
The theory of inflation also predicts that the sound waves should have nearly the same amplitude on all scales. The power spectrum, however, shows a sharp drop-off in the magnitude of temperature variations after the third peak. This discrepancy can be explained by the fact that sound waves with short wavelengths dissipate. Because sound is carried by the collisions of particles in gas or plasma, a wave cannot propagate if its wavelength is shorter than the typical distance traveled by particles between collisions. In air, this distance is a negligible 10-5 centimeter. But in the primordial plasma just before recombination, a particle would typically travel some 10,000 light-years before striking another. (The universe at this stage was dense only in comparison with the modern universe, which is about a billion times as rarefied.) As measured today, after its 1,000- fold expansion, that scale is about 10 million light-years. Therefore, the amplitudes of the peaks in the power spectrum are damped below about 10 times this scale.
Just as musicians can distinguish a world-class violin from an ordinary one by the richness of its overtones, cosmologists can elucidate the shape and composition of the universe by examining the fundamental frequency of the primordial sound waves and the strength of the overtones. The CMB reveals the angular size of the most intense temperature variations — how large these hot and cold spots appear across the sky‚ &mdash which in turn tells us the frequency of the fundamental sound wave. Cosmologists can precisely estimate the actual size of this wave at the time of recombination because they know how quickly sound propagated in the primordial plasma. Likewise, researchers can determine the distance CMB photons have traveled before reaching Earth‚ &mdash about 45 billion light-years. (Although the photons have traveled for only about 14 billion years, the expansion of the universe has elongated their route.)
So cosmologists have complete information about the triangle formed by the wave and can check whether its angles add up to 180 degrees &mdash the classic test of spatial curvature. They do so to high precision, showing that aside from the overall expansion, the universe obeys the laws of Euclidean geometry and must be very close to spatially flat. And because the geometry of the universe depends on its energy density, this finding implies that the average energy density is close to the so-called critical density — about 10-29 gram per cubic centimeter.
The next thing cosmologists would like to know is the exact breakdown of the universe — matter and energy. The amplitudes of the overtones provide the key. Whereas ordinary sound waves are driven solely by gas pressure, the sound waves in the early universe were modified by the force of gravity. Gravity compresses the gas in denser regions and, depending on the phase of the sound wave, can alternately enhance or counteract sonic compression and rarefaction. Analyzing the modulation of the waves reveals the strength of gravity, which in turn indicates the matter-energy composition of the medium. As in today's universe, matter in the early universe fell into two main categories: baryons (protons and neutrons), which make up the bulk of so-called ordinary matter, and cold dark matter, which exerts gravity but has never been directly observed because it does not interact with ordinary matter or light in any noticeable way. Both ordinary matter and dark matter supply mass to the primordial gas and enhance the gravitational pull, but only ordinary matter undergoes the sonic compressions and rarefactions. At recombination, the fundamental wave is frozen in a phase where gravity enhances its compression of the denser regions of gas

Gravity and sonic motion work together: Influence of dark matter modulates the acoustic signals in the CMB. After inflation, denser regions of dark matter that have the same scale as the fundamental wave (represented as troughs in this potential-energy diagram) pull in baryons and photons by gravitational attraction. (The troughs are shown in ed because gravity also reduces the temperature of any escaping photons.) By the time of recombination, about 380,000 years later, gravity and sonic motion have worked together to raise the radiation temperature in the troughs (blue) and lower the temperature at the peaks (red). But the first overtone, which has half the fundamental wavelength, is caught in the opposite phase — gravity is attempting to compress the plasma while gas pressure is trying to expand it. As a result, the temperature variations caused by this overtone will be less pronounced than those caused by the fundamental wave.
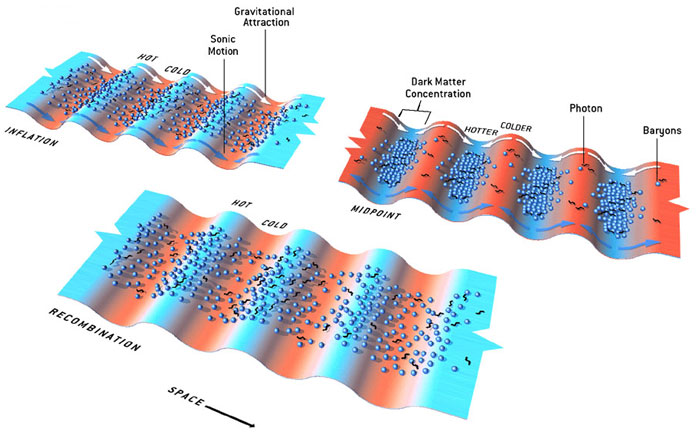
Gravity counteracts sonic motion: At smaller scales, gravity and acoustic pressure sometimes end up at odds. Dark matter clumps corresponding to a second-peak wave maximize radiation temperature in the troughs long before recombination. After this midpoint, gas pressure pushes baryons and photons out of the troughs (blue arrows) while gravity tries to pull them back in (white arrows). This tug-of-war decreases the temperature differences, which explains why the second peak in the power spectrum is lower than the first.
This effect explains why the second peak in the power spectrum is lower than the first. And by comparing the heights of the two peaks, cosmologists can gauge the relative strengths of gravity and radiation pressure in the early universe. This measurement indicates that baryons had about the same energy density as photons at the time of recombination and hence constitute about 5 percent of the critical density today. The result is in spectacular agreement with the number derived from studies of light-element synthesis by nuclear reactions in the infant universe.
The general theory of relativity, however, tells us that matter and energy gravitate alike. So did the gravity of the photons in the early universe also enhance the temperature variations? It did, in fact, but another effect counterbalanced it. After recombination, the CMB photons from denser regions lost more energy than photons from less dense areas, because they were climbing out of deeper gravitational-potential wells. This process, called the Sachs-Wolfe effect, reduced the amplitude of the temperature variations in the CMB, exactly negating the enhancement caused by the gravity of the photons. For regions of the early universe that were too big to undergo acoustic oscillations &mdash that is, regions stretching more than one degree across the sky &mdash temperature variations are solely the result of the Sachs-Wolfe effect. At these scales, paradoxically, hot spots in the CMB represent less dense regions of the universe.
Finally, cosmologists can use the CMB to measure the proportion of dark matter in the universe. The gravity from baryons alone could not have modulated the temperature variations much beyond the first peak in the power spectrum. An abundance of cold dark matter was needed to keep the gravitational-potential wells sufficiently deep. By measuring the ratios of the heights of the first three peaks, researchers have determined that the density of cold dark matter must be roughly five times the baryon density. Therefore, dark matter constitutes about 25 percent of the critical density today.
Unfortunately, these calculations of the modern universe's matter and energy leave about 70 percent of the critical density unspecified. To make up the difference, theorists have posited a mysterious component called dark energy, whose relative influence has grown as the universe has expanded. We are thus led by degrees to an improbable conclusion: most of the universe today is composed of invisible dark matter and dark energy. Worse yet, dark matter and dark energy seem to be coincidentally comparable in energy density today, even though the former vastly outweighed the latter at recombination. Physicists dislike coincidences; they prefer to explain the world in terms of cause and effect rather than dumb luck. What is more, another mysterious component, the inflaton, dominated the very early universe and seeded cosmic structure. Why should we believe a cosmological model that is based on the seemingly fanciful introduction of three enigmatic entities?
One reason is that these three entities explain a wealth of previously known facts. Dark matter was first postulated in the 1930s to explain measurements of the local mass density in galaxy clusters. Albert Einstein introduced the concept of dark energy in 1917 when he included the so-called cosmological constant in his equations to counteract the influence of gravity. He later disavowed the constant, but it was resurrected in the 1990s, when observations of distant supernovae showed that the expansion of the universe is accelerating. The energy densities of dark matter and dark energy, as measured from the CMB, are in striking accord with these astronomical observations.
Second, the standard cosmological model has predictive power. In 1968 Joseph Silk (now at the University of Oxford) predicted that the small-scale acoustic peaks in the CMB should be damped in a specific, calculable way. As a result, the corresponding radiation should gain a small but precisely known polarization. (Polarized radiation is oriented in a particular direction.) One might assume that the CMB would be unpolarized because the scattering of the photons in the primordial plasma would have randomized their direction. But on the small scales where damping occurs, photons can travel with relatively few scatterings, so they retain directional information that is imprinted as a polarization of the CMB. This acoustic polarization was measured by the Degree Angular Scale Interferometer (an instrument operated at the Amundsen-Scott South Pole Station in Antarctica) and later by WMAP; the value was in beautiful agreement with predictions. WMAP also detected polarization on larger scales that was caused by scattering of CMB photons after recombination.
Furthermore, the existence of dark energy predicts additional phenomena in the CMB that are beginning to be observed. Because dark energy accelerates the expansion of the universe, it weakens the gravitational-potential wells associated with the clustering of galaxies. A photon traveling through such a region gets a boost in energy as it falls into the potential well, but because the well is shallower by the time the photon climbs back out, it loses less energy than it previously gained. This phenomenon, called the integrated Sachs-Wolfe effect, causes large-scale temperature variations in the CMB. Observers have recently seen hints of this correlation by comparing large structures in galaxy surveys with the WMAP data. The amount of dark energy needed to produce the large-scale temperature variations is consistent with the amount inferred from the acoustic peaks and the distant supernovae. As the data from the galaxy surveys improve and other tracers of the large-scale structure of the universe become available, the integrated Sachs-Wolfe effect could become an important source of information about dark energy.
The CMB may also provide crucial new evidence that could explain what happened during the very first moments after the big bang. Few aspects of cosmology are more bizarre than the period of inflation. Did the universe really inflate, and, if so, what was the nature of the inflaton, the theoretical field that caused the rapid expansion? Current measurements of the CMB have dramatically strengthened the case for the simplest models of inflation, which assume that the amplitudes of the initial density fluctuations were nearly the same at all scales. But if more detailed observations of the CMB reveal that the amplitudes varied at different scales, the simple inflation models would be in trouble. More baroque alternatives would need to be invoked or altogether different paradigms adopted.
Another exciting possibility is that we could learn about the physics of inflation by determining the energy scale at which it took place. For example, physicists believe that the weak nuclear force and the electromagnetic force were different aspects of a single electroweak force when the universe was hotter than 1015 kelvins. If researchers determine that inflation occurred at this energy scale, it would strongly imply that the inflaton had something to do with electroweak unification. Alternatively, inflation could have occurred at the much higher temperatures at which the electroweak force merges with the strong nuclear force. In this case, inflation would most likely be associated with the grand unification of the fundamental forces.
A distinctive signature in the CMB could allow researchers to settle this issue. In addition to spawning density perturbations, inflation created fluctuations in the fabric of spacetime itself. These fluctuations are gravitational waves whose wavelengths can stretch across the observable universe. The amplitude of these gravitational waves is proportional to the square of the energy scale at which inflation took place. If inflation occurred at the high energies associated with grand unification, the effects might be visible in the polarization of the CMB.
Last, further observations of the CMB could shed some light on the physical nature of dark energy. This entity might be a form of vacuum energy, as Einstein had hypothesized, but its value would have to be at least 60 and perhaps as much as 120 orders of magnitude as small as that predicted from particle physics. And why is dark energy comparable to dark matter in density now and apparently only now? To answer these questions, researchers can take advantage of the fact that CMB photons illuminate structures across the entire observable universe. By showing the amplitude of density fluctuations at different points in cosmic history, the CMB can reveal the tug-of-war between matter and dark energy.
Measurements of two CMB phenomena could be particularly useful. The first, called the Sunyaev-Zel'dovich effect, occurs when CMB photons are scattered by the hot ionized gas in galaxy clusters. This effect allows galaxy clusters to be identified during the crucial period, about five billion years ago, when dark energy began to accelerate the expansion of the universe. The number of galaxy clusters, in turn, indicates the amplitude of density fluctuations during this time. The second phenomenon, gravitational lensing, happens when CMB photons pass by a particularly massive structure that bends their trajectories and hence distorts the pattern of temperature and polarization variations. The degree of lensing reveals the amplitude of the mass density fluctuations associated with these structures.
To conduct these investigations of inflation and dark energy, however, researchers will need a new generation of CMB telescopes that can observe the radiation with even greater sensitivity and resolution. In 2007 the European Space Agency plans to launch the Planck spacecraft, a microwave observatory that will be placed in the same orbit as WMAP. Planck will be able to measure CMB temperature differences as small as five millionths of a kelvin and detect hot and cold spots that subtend less than a tenth of a degree across the sky. Such measurements will enable scientists to glimpse the full range of acoustic oscillations in the CMB and thus sharpen their picture of the inflationary spectrum. A multitude of ground-based experiments are also under way to study CMB effects associated with structure in the current epoch of accelerated expansion.
Although the standard cosmological model appears to work remarkably well as a phenomenological description of the universe, a deeper understanding of its mysteries awaits the findings of these experiments. It seems clear that the cosmic symphony will continue to enchant its listeners for some time to come.