
Just as musicians can distinguish a world-class violin from an ordinary one by the richness of its overtones, cosmologists can elucidate the shape and composition of the universe by examining the fundamental frequency of the primordial sound waves and the strength of the overtones. The CMB reveals the angular size of the most intense temperature variations — how large these hot and cold spots appear across the sky — which in turn tells us the frequency of the fundamental sound wave. Cosmologists can precisely estimate the actual size of this wave at the time of recombination because they know how quickly sound propagated in the primordial plasma. Likewise, researchers can determine the distance CMB photons have traveled before reaching Earth &mdash about 45 billion light-years. (Although the photons have traveled for only about 14 billion years, the expansion of the universe has elongated their route.)
So cosmologists have complete information about the triangle formed by the wave and can check whether its angles add up to 180 degrees &mdash the classic test of spatial curvature. They do so to high precision, showing that aside from the overall expansion, the universe obeys the laws of Euclidean geometry and must be very close to spatially flat. And because the geometry of the universe depends on its energy density, this finding implies that the average energy density is close to the so-called critical density — about 10-29 gram per cubic centimeter.
The next thing cosmologists would like to know is the exact breakdown of the universe — matter and energy. The amplitudes of the overtones provide the key. Whereas ordinary sound waves are driven solely by gas pressure, the sound waves in the early universe were modified by the force of gravity. Gravity compresses the gas in denser regions and, depending on the phase of the sound wave, can alternately enhance or counteract sonic compression and rarefaction. Analyzing the modulation of the waves reveals the strength of gravity, which in turn indicates the matter-energy composition of the medium. As in today's universe, matter in the early universe fell into two main categories: baryons (protons and neutrons), which make up the bulk of so-called ordinary matter, and cold dark matter, which exerts gravity but has never been directly observed because it does not interact with ordinary matter or light in any noticeable way. Both ordinary matter and dark matter supply mass to the primordial gas and enhance the gravitational pull, but only ordinary matter undergoes the sonic compressions and rarefactions. At recombination, the fundamental wave is frozen in a phase where gravity enhances its compression of the denser regions of gas

Gravity and sonic motion work together: Influence of dark matter modulates the acoustic signals in the CMB. After inflation, denser regions of dark matter that have the same scale as the fundamental wave (represented as troughs in this potential-energy diagram) pull in baryons and photons by gravitational attraction. (The troughs are shown in ed because gravity also reduces the temperature of any escaping photons.) By the time of recombination, about 380,000 years later, gravity and sonic motion have worked together to raise the radiation temperature in the troughs (blue) and lower the temperature at the peaks (red). But the first overtone, which has half the fundamental wavelength, is caught in the opposite phase — gravity is attempting to compress the plasma while gas pressure is trying to expand it. As a result, the temperature variations caused by this overtone will be less pronounced than those caused by the fundamental wave.
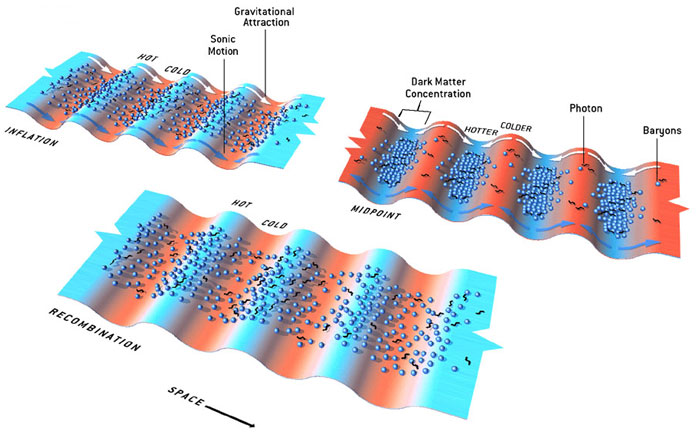
Gravity counteracts sonic motion: At smaller scales, gravity and acoustic pressure sometimes end up at odds. Dark matter clumps corresponding to a second-peak wave maximize radiation temperature in the troughs long before recombination. After this midpoint, gas pressure pushes baryons and photons out of the troughs (blue arrows) while gravity tries to pull them back in (white arrows). This tug-of-war decreases the temperature differences, which explains why the second peak in the power spectrum is lower than the first.
This effect explains why the second peak in the power spectrum is lower than the first. And by comparing the heights of the two peaks, cosmologists can gauge the relative strengths of gravity and radiation pressure in the early universe. This measurement indicates that baryons had about the same energy density as photons at the time of recombination and hence constitute about 5 percent of the critical density today. The result is in spectacular agreement with the number derived from studies of light-element synthesis by nuclear reactions in the infant universe.
The general theory of relativity, however, tells us that matter and energy gravitate alike. So did the gravity of the photons in the early universe also enhance the temperature variations? It did, in fact, but another effect counterbalanced it. After recombination, the CMB photons from denser regions lost more energy than photons from less dense areas, because they were climbing out of deeper gravitational-potential wells. This process, called the Sachs-Wolfe effect, reduced the amplitude of the temperature variations in the CMB, exactly negating the enhancement caused by the gravity of the photons. For regions of the early universe that were too big to undergo acoustic oscillations &mdash that is, regions stretching more than one degree across the sky &mdash temperature variations are solely the result of the Sachs-Wolfe effect. At these scales, paradoxically, hot spots in the CMB represent less dense regions of the universe.
Finally, cosmologists can use the CMB to measure the proportion of dark matter in the universe. The gravity from baryons alone could not have modulated the temperature variations much beyond the first peak in the power spectrum. An abundance of cold dark matter was needed to keep the gravitational-potential wells sufficiently deep. By measuring the ratios of the heights of the first three peaks, researchers have determined that the density of cold dark matter must be roughly five times the baryon density. Therefore, dark matter constitutes about 25 percent of the critical density today.