semi-minor axis as the spatial phase changes from crest
trough (see Fig. 7, yellow ellipses).
Heuristically, the accompanying stretching of the wavelength of photons
produces a quadrupolar temperature variation with an 
pattern
Tensor fluctuations are transverse-traceless perturbations to the metric,
which can be viewed as gravitational waves. A plane gravitational wave
perturbation represents a quadrupolar ``stretching'' of space in the plane
of the perturbation (see Fig. 7).
As the wave passes or its amplitude changes, a circle of test particles in
the plane is distorted into an ellipse whose semi-major axis
semi-minor axis as the spatial phase changes from crest
trough (see Fig. 7, yellow ellipses).
Heuristically, the accompanying stretching of the wavelength of photons
produces a quadrupolar temperature variation with an pattern
in the coordinates defined by 
.
Fig. 7: The tensor quadrupole moment (l=2, m=2). Since gravity waves distort space in the plane of the perturbation, changing a circle of test particles into an ellipse, the radiation acquires an m=2 quadrupole moment.
Thomson scattering again produces a polarization pattern from the quadrupole
anisotropy. At the equator, the quadrupole pattern intersects the tangent
( 
) plane with hot and cold lobes rotating
in and out of the 
direction with the azimuthal angle 
.
The polarization pattern is therefore purely Q with a 
dependence.
At the pole, the quadrupole lobes lie completely in the polarization plane
and produces the maximal polarization unlike the scalar and vector cases.
The full pattern,
is shown in Fig. 8 (real part). Note that Q and U are present in nearly equal amounts for the tensors.
Fig. 8: Polarization pattern for l=2, m=2. Scattering of a tensor perturbation generates the E pattern (yellow, thick lines) as opposed to the B (purple, thin lines) pattern.
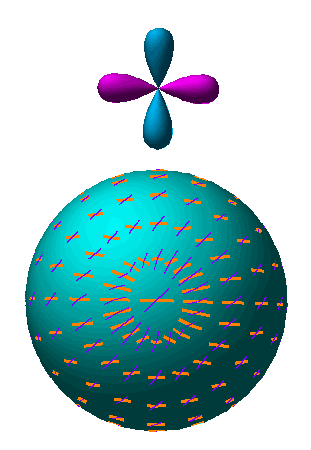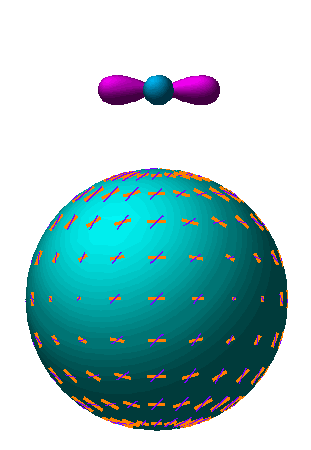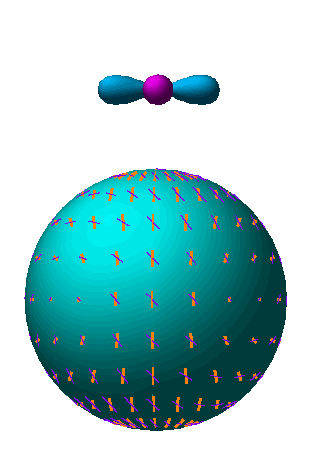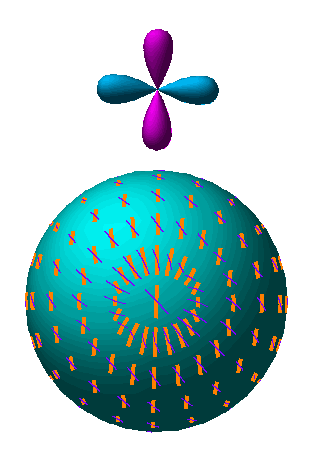
Animation: Same as for scalars.
Next: Polarization Patterns