• Review Home
• Introduction
• Observables
  • Cosmological Paradigm
  • Temperature Field
  • Polarization Field
• Acoustic Peaks
  • Introduction
  • Basics
  • Initial Conditions
  • Gravitational Forcing
  • Baryon Loading
  • Radiation Driving
  • Damping
  • Polarization
  • Integral Approach
  • Parameter Sensitivity
• Matter Power Spectrum
  • Introduction
  • Physical Description
  • Cosmological Implications
• Gravitational Secondaries
  • Introduction
  • ISW Effect
  • RS/Moving Halo
  • Gravitational Waves
  • Gravitational Lensing
• Scattering Secondaries
  • Introduction
  • Peak Suppression
  • Large Angle Polarization
  • Doppler Effect
  • Modulated Doppler Effect
  • SZ Effect
• Non-Gaussianity
• Data Analysis
  • Introduction
  • Mapmaking
  • Bandpower Estimation
  • Parameter Estimation
• Discussion
  • Discussion
  • Bibliography

Integral Approach

The discussion in the previous sections suffices for a qualitative understanding of the acoustic peaks in the power spectra of the temperature and polarization anisotropies. To refine this treatment we must consider more carefully the sources of anisotropies and their projection into multipole moments.

Because the description of the acoustic oscillations takes place in Fourier space, the projection of inhomogeneities at recombination onto anisotropies today has an added level of complexity. An observer today sees the acoustic oscillations in effective temperature as they appeared on a spherical shell at at recombination, where is the direction vector, and is the distance light can travel between recombination and the present (see Plate 3). Having solved for the Fourier amplitude , we can expand the exponential in Equation (6) in terms of spherical harmonics, so the observed anisotropy today is

(21)

where the projected source . Because the spherical harmonics are orthogonal, Equation (1) implies that today is given by the integral in square brackets today. A given plane wave actually produces a range of anisotropies in angular scale as is obvious from Plate 3. The one-to-one mapping between wavenumber and multipole moment described in §3.1 is only approximately true and comes from the fact that the spherical Bessel function is strongly peaked at . Notice that this peak corresponds to contributions in the direction orthogonal to the wavevector where the correspondence between and is one-to-one (see Plate 3).

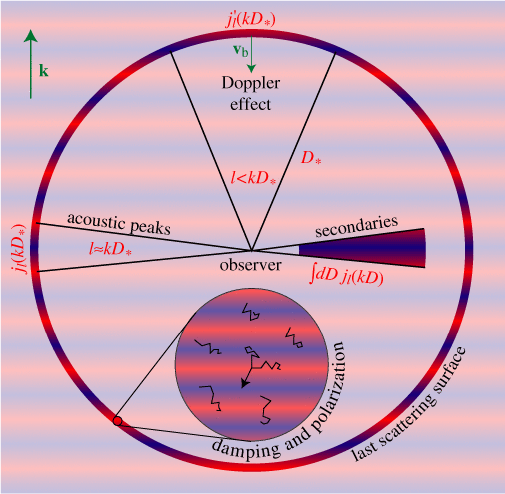
Projection is less straightforward for other sources of anisotropy. We have hitherto neglected the fact that the acoustic motion of the photon-baryon fluid also produces a Doppler shift in the radiation that appears to the observer as a temperature anisotropy as well. In fact, we argued above that is of comparable magnitude but out of phase with the effective temperature. If the Doppler effect projected in the same way as the effective temperature, it would wash out the acoustic peaks. However, the Doppler effect has a directional dependence as well since it is only the line-of-sight velocity that produces the effect. Formally, it is a dipole source of temperature anisotropies and hence has an structure. The coupling of the dipole and plane wave angular momenta imply that in the projection of the Doppler effect involves a combination of that may be rewritten as . The structure of lacks a strong peak at . Physically this corresponds to the fact that the velocity is irrotational and hence has no component in the direction orthogonal to the wavevector (see Plate 3). Correspondingly, the Doppler effect cannot produce strong peak structures [Hu & Sugiyama, 1995]. The observed peaks must be acoustic peaks in the effective temperature not ``Doppler peaks''.

There is one more subtlety involved when passing from acoustic oscillations to anisotropies. Recall from §3.5 that radiation leads to decay of the gravitational potentials. Residual radiation after decoupling therefore implies that the effective temperature is not precisely . The photons actually have slightly shallower potentials to climb out of and lose the perturbative analogue of the cosmological redshift, so the overestimates the difference between the true photon temperature and the observed temperature. This effect of course is already in the continuity equation for the monopole Equation (18) and so the source in Equation (21) gets generalized to

(22)

The last term vanishes for constant gravitational potentials, but is non-zero if residual radiation driving exists, as it will in low models. Note that residual radiation driving is particularly important because it adds in phase with the monopole: the potentials vary in time only near recombination, so the Bessel function can be set to and removed from the integral. This complication has the effect of decreasing the multipole value of the first peak as the matter-radiation ratio at recombination decreases [Hu & Sugiyama, 1995]. Finally, we mention that time varying potentials can also play a role at very late times due to non-linearities or the importance of a cosmological constant for example. Those contributions, to be discussed more in §4.2.1, are sometimes referred to as late Integrated Sachs-Wolfe effects, and do not add coherently with .

Putting these expressions together and squaring, we obtain the power spectrum of the acoustic oscillations

(23)

This formulation of the anisotropies in terms of projections of sources with specific local angular structure can be completed to include all types of sources of temperature and polarization anisotropies at any given epoch in time linear or non-linear: the monopole, dipole and quadrupole sources arising from density perturbations, vorticity and gravitational waves [Hu & White, 1997b]. In a curved geometry one replaces the spherical Bessel functions with ultraspherical Bessel functions [Abbott & Schaefer, 1986,Hu et al, 1998]. Precision in the predictions of the observables is then limited only by the precision in the prediction of the sources. This formulation is ideal for cases where the sources are governed by non-linear physics even though the CMB responds linearly as we shall see in §4.

Perhaps more importantly, the widely-used CMBFAST code [Seljak & Zaldarriaga, 1996] exploits these properties to calculate the anisotropies in linear perturbation efficiently. It numerically solves for the smoothly-varying sources on a sparse grid in wavenumber, interpolating in the integrals for a handful of 's in the smoothly varying . It has largely replaced the original ground breaking codes [Wilson & Silk, 1981,Bond & Efstathiou, 1984,Vittorio & Silk, 1984] based on tracking the rapid temporal oscillations of the multipole moments that simply reflect structure in the spherical Bessel functions themselves.