blackboard

waynehu

Professor, Department of Astronomy and Astrophysics
University of Chicago

Group Contact CV SnapShots
CMB Introduction '96   Intermediate '01   Polarization Intro '01   Cosmic Symphony '04   Polarization Primer '97   Review '02   Power Animations   Lensing   Power Prehistory   Legacy Material '96   PhD Thesis '95 Baryon Acoustic Oscillations Cosmic Shear Clusters
Transfer Function
Intro to Cosmology [243] Cosmology I [legacy 321] Cosmology II [321] Current Topics [282] Galaxies and Universe [242] Radiative Processes [305] Research Preparation [307] GR Perturbation Theory [408] CMB [448] Cosmic Acceleration [449]

CMB Temperature Field

The basic observable of the CMB is its intensity as a function of frequency and direction on the sky $\hat {\bf n}$. Since the CMB spectrum is an extremely good blackbody [Fixsen et al, 1996] with a nearly constant temperature across the sky T, we generally describe this observable in terms of a temperature fluctuation $\Theta(\hat {\bf n}) = \Delta T/T$.

If these fluctuations are Gaussian, then the multipole moments of the temperature field

\begin{displaymath} \Theta_{\ell m} = \int d{\hat {\bf n}} Y_{\ell m}^*(\hat {\bf n}) \Theta(\hat {\bf n}) \end{displaymath} (1)

are fully characterized by their power spectrum

\begin{displaymath} \left< \Theta_{\ell m}^{*} \Theta_{\ell'm'} \right> = \delta_{\ell \ell'}\delta_{m m'} C_{\ell}\,, \end{displaymath} (2)

whose values as a function of l are independent in a given realization. For this reason predictions and analyses are typically performed in harmonic space. On small sections of the sky where its curvature can be neglected, the spherical harmonic analysis becomes ordinary Fourier analysis in two dimensions. In this limit l becomes the Fourier wavenumber. Since the angular wavelength &theta=2&pi/l, large multipole moments corresponds to small angular scales with l~102 representing degree scale separations. Likewise, since in this limit the variance of the field is &int d2l Cl/(2π)2, the power spectrum is usually displayed as

\begin{displaymath} \Delta_T^2 \equiv {\ell(\ell+1) \over 2\pi} C_\ell T^2\,, \end{displaymath} (3)

the power per logarithmic interval in wavenumber for l>>1.

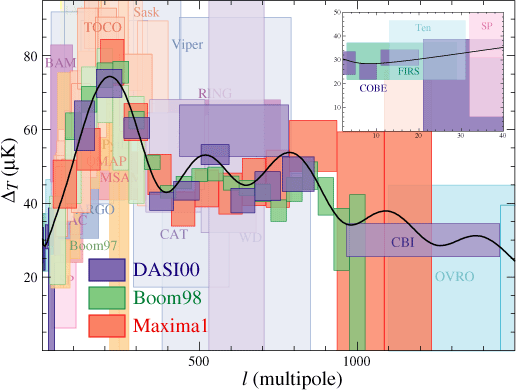
Plate 1 (top) shows observations of &DeltaT along with the prediction of the working cosmological model, complete with the acoustic peaks mentioned in §1 and discussed extensively in §3. While COBE first detected anisotropy on the largest scales (inset), observations in the last decade have pushed the frontier to smaller and smaller scales (left to right in the figure). The MAP satellite, launched in June 2001, will go out to l~1000, while the European satellite, Planck, scheduled for launch in 2007, will go a factor of two higher (see Plate 1 bottom).

The power spectra shown in Plate 1 all begin at l=2 and exhibit large errors at low multipoles. The reason is that the predicted power spectrum is the average power in the multipole moment l an observer would see in an ensemble of universes. However a real observer is limited to one Universe and one sky with its one set of &Thetalm, 2l+1 numbers for each l. This is particularly problematic for the monopole and dipole (l=0,1). If the monopole were larger in our vicinity than its average value, we would have no way of knowing it. Likewise for the dipole, we have no way of distinguishing a cosmological dipole from our own peculiar motion with respect to the CMB rest frame. Nonetheless, the monopole and dipole - which we will often call simply &Theta and v&gamma - are of the utmost significance in the early Universe. It is precisely the spatial and temporal variation of these quantities, especially the monopole, which determines the pattern of anisotropies we observe today. A distant observer sees spatial variations in the local temperature or monopole, at a distance given by the lookback time, as a fine-scale angular anisotropy. Similarly, local dipoles appear as a Doppler shifted temperature which is viewed analogously. In the jargon of the field, this simple projection is referred to as the freestreaming of power from the monopole and dipole to higher multipole moments.


\begin{plate} % latex2html id marker 183 %%3 \centerline{\epsfxsize=4.75in\epsff... ...and boxes represent the statistical errors of the Planck satellite.}\end{plate}


Table 1: CMB experiments shown in Plate 1 and references.
Name Authors Journal Reference
ARGO Masi S et al. 1993 Ap. J. Lett. 463:L47-L50
ATCA Subrahmanyan R et al. 2000 MNRAS 315:808-822
BAM Tucker GS et al. 1997 Ap. J. Lett. 475:L73-L76
BIMA Dawson KS et al. 2001 Ap. J. Lett. 553:L1-L4
BOOM97 Mauskopf PD et al. 2000 Ap. J. Lett. 536:L59-L62
BOOM98 Netterfield CB et al. 2001 Ap. J. In press
CAT99 Baker JC et al. 1999 MNRAS 308:1173-1178
CAT96 Scott PF et al. 1996 Ap. J. Lett. 461:L1-L4
CBI Padin S et al. 2001 Ap. J. Lett. 549:L1-L5
COBE Hinshaw G, et al. 1996 Ap. J. 464:L17-L20
DASI Halverson NW et al. 2001 Ap. J. In press
FIRS Ganga K, et al. 1994. Ap. J. Lett. 432:L15-L18
IAC Dicker SR et al. 1999 Ap. J. Lett. 309:750-760
IACB Femenia B, et al. 1998 Ap. J. 498:117-136
QMAP de Oliveira-Costa A et al. 1998 Ap. J. Lett. 509:L77-L80
MAT Torbet E et al. 1999 Ap. J. Lett. 521:L79-L82
MAX Tanaka ST et al. 1996 Ap. J. Lett. 468:L81-L84
MAXIMA1 Lee AT et al. 2001 Ap. J. In press
MSAM Wilson GW et al. 2000 Ap. J. 532:57-64
OVRO Readhead ACS et al. 1989 Ap. J. 346:566-587
PYTH Platt SR et al. 1997 Ap. J. Lett. 475:L1-L4
PYTH5 Coble K et al. 1999 Ap. J. Lett. 519:L5-L8
RING Leitch EM et al. 2000 Ap. J. 532:37-56
SASK Netterfield CB et al. 1997 Ap. J. Lett. 477:47-66
SP94 Gunderson JO, et al. 1995 Ap. J. Lett. 443:L57-L60
SP91 Schuster J et al. 1991 Ap. J. Lett. 412:L47-L50
SUZIE Church SE et al. 1997 Ap. J. 484:523-537
TEN Gutiérrez CM, et al. 2000 Ap. J. Lett. 529:47-55
TOCO Miller AD et al. 1999 Ap. J. Lett. 524:L1-L4
VIPER Peterson JB et al. 2000 Ap. J. Lett. 532:L83-L86
VLA Partridge RB et al. 1997 Ap. J. 483:38-50
WD Tucker GS et al. 1993 Ap. J. Lett. 419:L45-L49
MAP http://map.nasa.gsfc.gov
Planck http://astro.estec.esa.nl/Planck


How accurately can the spectra ultimately be measured? As alluded to above, the fundamental limitation is set by ``cosmic variance'' the fact that there are only $2\ell+1$ $m$-samples of the power in each multipole moment. This leads to an inevitable error of

$\displaystyle \Delta C_\ell = \sqrt{2 \over 2 \ell +1} C_\ell \,.$
 (4)

Allowing for further averaging over $\ell $ in bands of $\Delta \ell \approx \ell$, we see that the precision in the power spectrum determination scales as $\ell^{-1}$, i.e. $\sim 1\%$ at $\ell=100$ and $\sim 0.1\%$ at $\ell=1000$. It is the combination of precision predictions and prospects for precision measurements that gives CMB anisotropies their unique stature.

There are two general caveats to these scalings. The first is that any source of noise, instrumental or astrophysical, increases the errors. If the noise is also Gaussian and has a known power spectrum, one simply replaces the power spectrum on the rhs of Equation (4) with the sum of the signal and noise power spectra [Knox, 1995]. This is the reason that the errors for the Planck satellite increase near its resolution scale in Plate 1 (bottom). Because astrophysical foregrounds are typically non-Gaussian it is usually also necessary to remove heavily contaminated regions, e.g. the galaxy. If the fraction of sky covered is $f_{\rm sky}$, then the errors increase by a factor of $f_{\rm sky}^{-1/2}$ and the resulting variance is usually dubbed ``sample variance'' [Scott et al, 1994]. An fsky=0.65 was chosen for the Planck satellite.

next up previous
Next: CMB Polarization Field Up: OBSERVABLES Previous: Standard Cosmological Paradigm
Wayne Hu 2001-10-15